四维双标量场理论的全循环共形杨振宁对称性

100 浏览量更新于2024-07-16 收藏 812KB PDF 举报

"这篇研究论文探讨了四维双标量场理论中的仰角对称性，特别是关于平面振幅的全回路共形仰角对称性。文章指出，这种理论是γ扭弱耦合N = 4超 Yang-Mills (SYM) 理论的一种特殊的双标度极限。双标量粒子的振幅通过渔网Feynman图来表示，这些图具有单一的圆盘拓扑结构，并从规则方格中切出。仰角的实现依赖于Lax算子在圆盘边界上对特定不均匀参数序列的作用。作者还成功地构建了一级Yangian生成元，用于明确表示通用双标量振幅。此外，文中也讨论了这些散射幅度与双重共形对称性的联系。" 这篇开放访问的学术文章发表在JHEP05(2018)003期刊上，涵盖了高能物理和理论物理学领域的研究。它在2017年12月12日提交，2018年4月22日接受，并于5月2日正式发布。由多位来自德国和法国的科学家共同撰写，他们分别隶属于PRISMA卓越集群、巴黎高等师范学院的理论物理实验室、柏林洪堡大学的物理研究所等多个知名机构。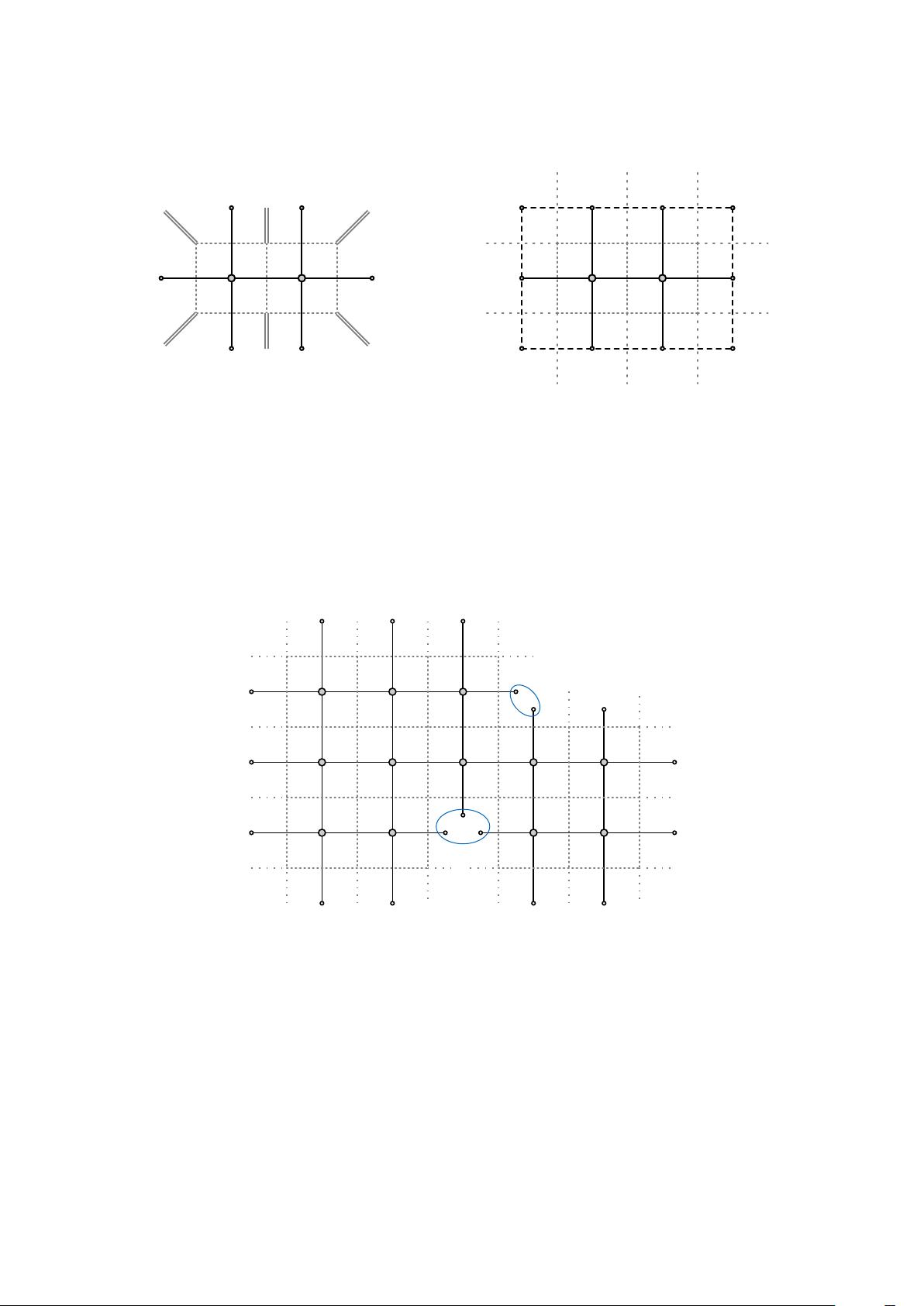文章的核心内容围绕着双标量环振幅的对称性展开。Yangians对称性是一种在量子场论中重要的数学结构，它扩展了对称群的概念，特别是在多环振幅的计算中扮演关键角色。在本文中，作者展示了如何在双标量场理论的全集振幅中建立全回路的共形Yangians对称性，这是通过对γ扭曲的N = 4 SYM理论进行双标度极限而得到的特殊理论。这个理论中，每个特定阶数的标量粒子振幅都由特定的Feynman图表示，这些图具有特定的几何特性，即单个圆盘拓扑结构，且与Lax算子相关联。 Lax算子在圆盘边界的使用是实现仰角对称性的重要工具，通过作用于特定的不均匀参数序列，可以揭示振幅的内在对称性。此外，作者还通过这种方法构造了一级的Yangian生成元，这有助于更深入理解和计算这些振幅。最后，他们探讨了这些散射振幅与双重共形对称性的关系，这是量子场论中另一个基本的对称原理，对于理解和简化复杂的物理过程至关重要。总而言之，这项工作深化了我们对四维双标量场理论的理解，特别是其内在的对称性和计算方法，为理论物理学的研究提供了新的视角和工具。

JHEP05(2018)003

Figure 4. Two-loop diagrams: double box topology in momentum variables (integration over

momenta ﬂowing in loops) and its dual double cross topology in region momentum variables (in-

tegration over position of the vertices — ﬁlled blobs). (A): all inﬂowing momenta (depicted by

double lines) are oﬀ shell, p

= x

i i+1

6= 0 at i = 1, . . . , 6. (B): amplitude diagram for scattering of

massless particles, i.e. the inﬂowing momenta (depicted by loosely dotted gray lines) are light-like

= x

i i+1

= 0 at i = 1, . . . , 10. These constraints are imposed by means of delta functions δ(x

i i+1

)

depicted by dashed black lines.

Figure 5. In this picture, a bi-scalar scattering amplitude of massless scalars is represented in the

dual graph depicted by dotted lines. It has doubled (w.r.t. the previous ﬁgure 2) external legs at the

convex corners of the boundary, and no legs at the concave corners. The corresponding additional

momentum variables at convex corners should satisfy the momentum conservation condition at each

dual vertex. We obtain the admissible bi-scalar amplitude by identifying the points of the boundary

of the original graph which end in the same square (i.e., the same site of the original lattice. Such

points are surrounded by ellipses in the above ﬁgure. The masslessness is ensured by additional

factors δ(p

) multiplying the external legs of the dual graph.

– 6 –

JHEP05(2018)003

the Feynman graphs under consideration (the “lasso” method). Then, expanding it with

respect to the spectral parameter, we obtain the level-one generators of the conformal

Yangian algebra and comment on its relation to dual conformal symmetry.

2 Yangian invariants and monodromy matrix

In this section we brieﬂy review the construction of Yangian invariants before specifying

it to the case of the conformal algebra so(2, 4). Historically, the so-called RTT realization

of the Yangian algebra ﬁrst appeared implicitly in the context of the quantum inverse

scattering method [23, 24], much earlier than its general deﬁnition by Drinfel’d. In this

framework, the Yangian commutation relations are encoded into a Yang-Baxter equation

for the monodromy matrix T (u), the so-called RTT-relation:

R(u − v) T (u) ⊗ T (v) = T (v) ⊗T (u) R(u − v) . (2.1)

The monodromy matrix T (u) is a formal series in the spectral parameter u. It encompasses

the inﬁnite set of Yangian generators J

(n)

αβ

[25]:

αβ

(u) = δ

αβ

∞

n=0

−n−1

(n)

αβ

. (2.2)

In the case of our interest, α, β = 1, . . . , 4 are matrix indices of the deﬁning representation

of su(2, 2) ≈ so(2, 4), and the numerical matrix R(u) is Yang’s R-matrix

R(u) = 1 + u P , (2.3)

where P is the permutation matrix. It satisﬁes the Yang-Baxter equation which is a consis-

tency relation for the structure constants of the Yangian algebra given by the RTT-relation.

The evaluation representation with J

(n)

= 0 for n > 0 provides the simplest solution

of (2.1), namely T

αβ

(u) = δ

αβ

+ u

−1

(0)

αβ

. For the case at hand, the J

(0)

αβ

are linear

combinations of the conformal algebra generators acting on a single site of a non-compact

spin chain. Up to a conventional overall factor of u we call the above solution the Lax

operator and denote it by L(u) ≡ uδ

αβ

+ J

(0)

αβ

The algebra given by the RTT-relation possesses a comultiplication structure. In par-

ticular, this means that the matrix product of several Lax operators (each acting on its

own spin chain site) respects (2.1). We thus ﬁnd that the inhomogeneous monodromy

T (~u) ' L

) . . . L

) speciﬁed by the set of parameters ~u = (u

, . . . , u

) fur-

nishes a solution of eq. (2.1). Here L

) acts on the i-th site of the spin chain.

As was shown in [26, 27], the eigenvalue problem for an inhomogeneous monodromy

constructed out of Lax operators, i.e.

) . . . L

) |λ; invi = λ(~u) |λ; invi1, (2.4)

provides a natural way to obtain Yangian invariants |λ; invi, which live on n sites of a non-

compact spin chain. Both sides of eq. (2.4) are matrices and 1 denotes the identity matrix.

– 7 –

剩余39页未读，继续阅读

weixin_38722193

粉丝: 5
资源: 908

四维双标量场理论的全循环共形杨振宁对称性

de Sitter上的无质量标量破坏了缩放对称性

具有高维标量表示和保管对称性的新型辐射中微子质量生成机理

标量引力振幅

标量可以具有渐近对称性吗？

D维双标量引力振幅的协变表达与经典广义相对论

标量部门的对称性和质量简并性

S 3对称标量扇区中的自发对称性破裂

寿命长的bino和wino与重标量和higgsinos超对称

来自标量振幅的共线极限的引力子振幅

双标量描述下土的弹性非线性损伤模型 (2007年)

最新资源