高级数据结构:AVL树与平衡二叉搜索树解析
需积分: 17 34 浏览量
更新于2024-08-01
收藏 498KB PDF 举报
"本资源主要讲解了高级数据结构在信息竞赛中的应用,由知名作者讲解,包括平衡二叉树、可并优先队列、线段树和树状数组的基础知识,以及RMQ(Range Minimum Query,范围最小值查询)和LCA(Lowest Common Ancestor,最近公共祖先)的概念。"
在信息竞赛和算法设计中,掌握高级数据结构是至关重要的。这些数据结构能够帮助我们高效地处理复杂的问题,提高算法的运行速度。以下是对这些高级数据结构的详细说明:
1. **平衡二叉树**:平衡二叉树是一种特殊的二叉树,其特点是任何节点的两个子树的高度差不超过1,这样可以确保树的平衡性,从而保证搜索、插入和删除等操作的时间复杂度接近最优,即O(logn)。不均衡的二叉树可能导致操作效率降低,例如极端情况下,树形退化成链表,操作时间复杂度将变为O(n)。
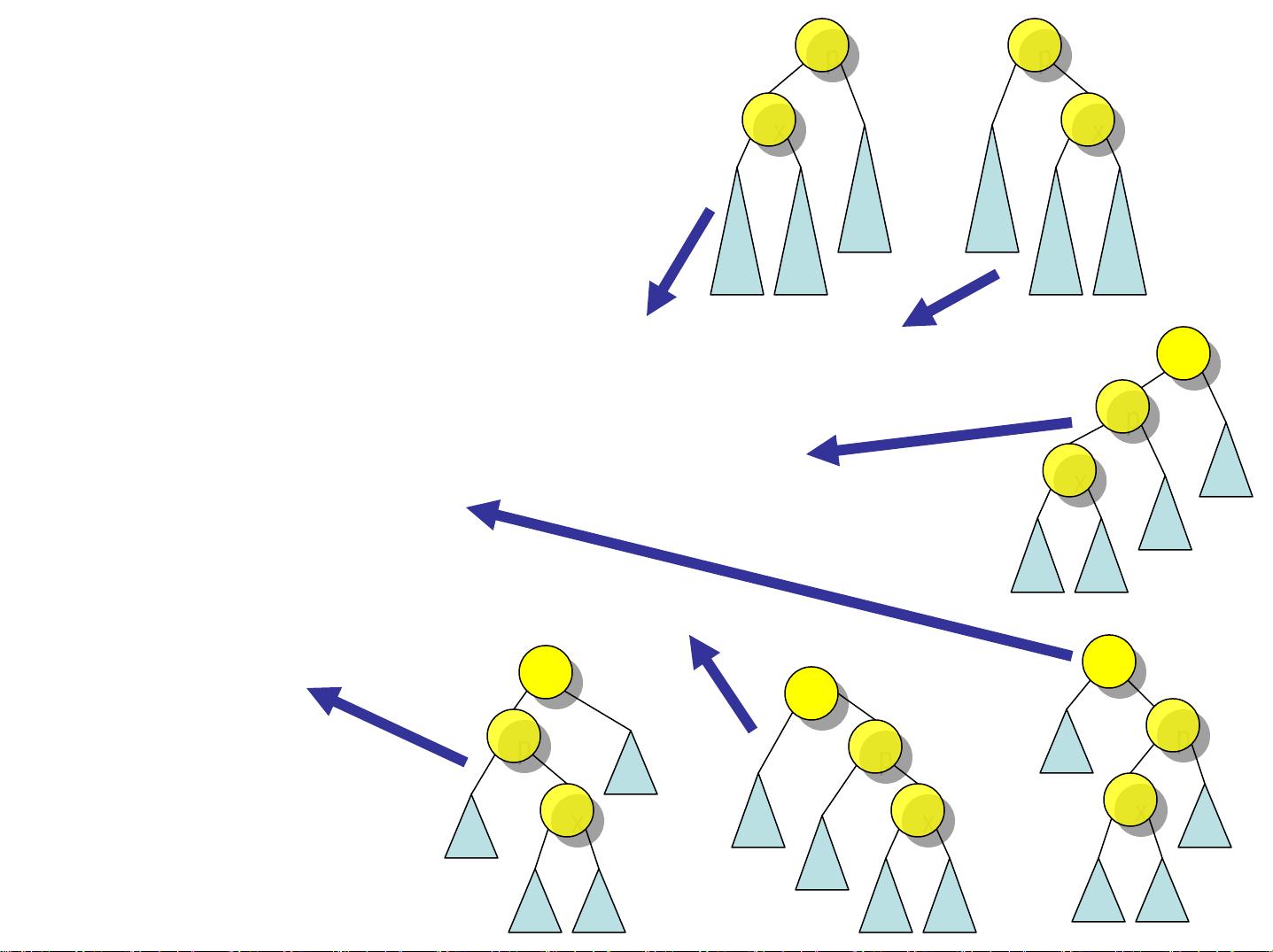
2. **AVL树**:AVL树是最早被提出的自平衡二叉搜索树,由Adelson-Velsky和Landis提出,故得名AVL树。AVL树要求每个节点的左右子树高度差不超过1,通过旋转操作(单旋和双旋)来维护平衡。插入和删除操作可能破坏平衡,这时就需要进行相应的旋转调整以恢复平衡。AVL树的高度保持在O(logn),保证了高效的查找性能。
- **AVL的单旋转**:当一个节点的左子树过高时,可以进行左旋;反之,如果右子树过高,则进行右旋。旋转操作用于调整树的结构,使其重新达到平衡。
- **AVL的双旋转**:当插入或删除导致不平衡且单旋转无法解决时,需要进行双旋转。双旋转包括先左旋再右旋或先右旋再左旋,以恢复树的平衡状态。
3. **可并优先队列**:可并优先队列是一种能高效合并和操作多个优先队列的数据结构,常用于解决堆合并问题,如Dijkstra最短路径算法。它的操作包括插入元素、合并队列和删除最小元素等,具有较高的效率。
4. **线段树和树状数组**:这两种数据结构主要用于区间操作,如求区间和、更新区间值等。线段树是树形结构,每个节点对应一个区间,支持快速查询和修改。树状数组(也叫斐波那契堆)则利用数组实现,通过懒惰标记和批量更新来优化区间操作。
5. **RMQ(Range Minimum Query)**:RMQ问题是询问一个数组区间内的最小值,通过预处理可以做到在线查询O(1)的时间复杂度。常见的解决方案有线段树、树状数组和Sqrt分解等。
6. **LCA(Lowest Common Ancestor)**:LCA问题是在树中找到两个节点的最近公共祖先,对于动态查询和树的遍历算法至关重要。常见算法有Morris遍历、LCA链剖、RMQ与LCA的结合等。
这些高级数据结构在信息竞赛和实际编程问题中有着广泛的应用,熟练掌握它们有助于解决复杂的问题,提高算法的效率。通过深入学习和实践,可以更好地理解和运用这些工具,提升编程能力。
2008-03-05 上传
2018-08-26 上传
点击了解资源详情
点击了解资源详情
2009-04-05 上传
2009-02-28 上传
2014-12-05 上传
2018-11-01 上传