> REPLACE THIS LINE WITH YOUR PAPER IDENTIFICATION NUMBER (DOUBLE-CLICK HERE TO EDIT) <
The step function format for exponential decay is:
(10)
The common practice is to use a learning rate decay of
to reduce the learning rate by a factor of 10 at each stage.
G. Weight decay
Weight decay is used for training deep learning models as the
L2 regularization approach, which helps to prevent over fitting
the network and model generalization. L2 regularization for
can be define as:
(11)
(12)
The gradient for the weight is:
(13)
General practice is to use the value . A smaller
will accelerate training.
Other necessary components for efficient training including
data preprocessing and augmentation, network initialization
approaches, batch normalization, activation functions,
regularization with dropout, and different optimization
approaches (as discussed in Section 4).
In the last few decades, many efficient approaches have been
proposed for better training of deep neural networks. Before
2006, attempts taken at training deep architectures failed: training
a deep supervised feed-forward neural network tended to yield
worse results (both in training and in test error) then shallow ones
(with 1 or 2 hidden layers). Hinton’s revolutionary work on
DBNs spearheaded a change in this in 2006 [50, 53].
Due to their composition, many layers of DNN are more
capable at representing highly varying nonlinear functions
compare to shallow learning approaches [56, 57, and 58].
Moreover, DNNs are more efficient for learning because of the
combination of feature extraction and classification layers. The
following sections discuss in detail about different DL
approaches with necessary components.
III. CONVOLUTIONAL NEURAL NETWORKS (CNN)
A. CNN overview
This network structure was first proposed by Fukushima in
1988 [48]. It was not widely used however due to limits of
computation hardware for training the network. In the 1990s,
LeCun et al. applied a gradient-based learning algorithm to
CNNs and obtained successful results for the handwritten digit
classification problem [49]. After that, researchers further
improved CNNs and reported state-of-the-art results in many
recognition tasks. CNNs have several advantages over DNNs,
including being more similar to the human visual processing
system, being highly optimized in structure for processing 2D
and 3D images, and being effective at learning and extracting
abstractions of 2D features. The max pooling layer of CNNs is
effective in absorbing shape variations. Moreover, composed of
sparse connections with tied weights, CNNs have significantly
fewer parameters than a fully connected network of similar size.
Most of all, CNNs are trained with the gradient-based learning
algorithm, and suffer less from the diminishing gradient
problem. Given that the gradient-based algorithm trains the
whole network to minimize an error criterion directly, CNNs
can produce highly optimized weights.
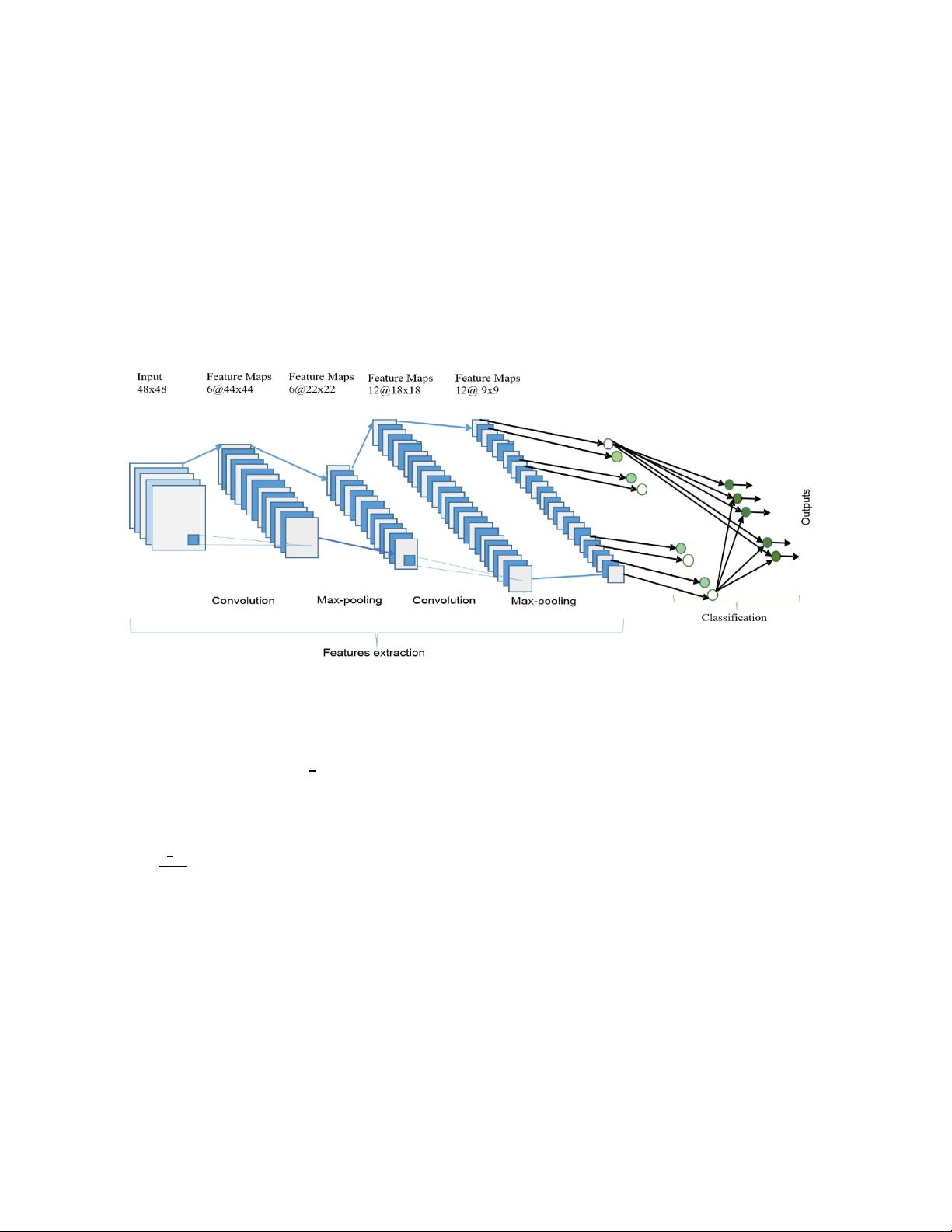
Fig. 11. The overall architecture of the CNN includes an input layer, multiple alternating convolution and max-pooling layers, one fully-connected
layer and one classification layer.










