小波变换入门教程:从基础到应用
下载需积分: 44 | PDF格式 | 1.32MB |
更新于2024-07-17
| 131 浏览量 | 举报
"小波变换经典讲述.pdf" 是一本针对小波变换初学者的入门教程,旨在解释这个相对较新的概念,让非专业数学背景的读者也能理解。教程作者指出,虽然小波变换的文献众多,但大部分对于新手来说难以理解。
小波变换是一种数学工具,用于分析信号和数据,它结合了时域和频域的优点,既能提供局部细节又能揭示信号的频率成分。在本教程中,作者将介绍小波变换的基本原理,而不涉及复杂的理论证明,以适应工程应用的需要。
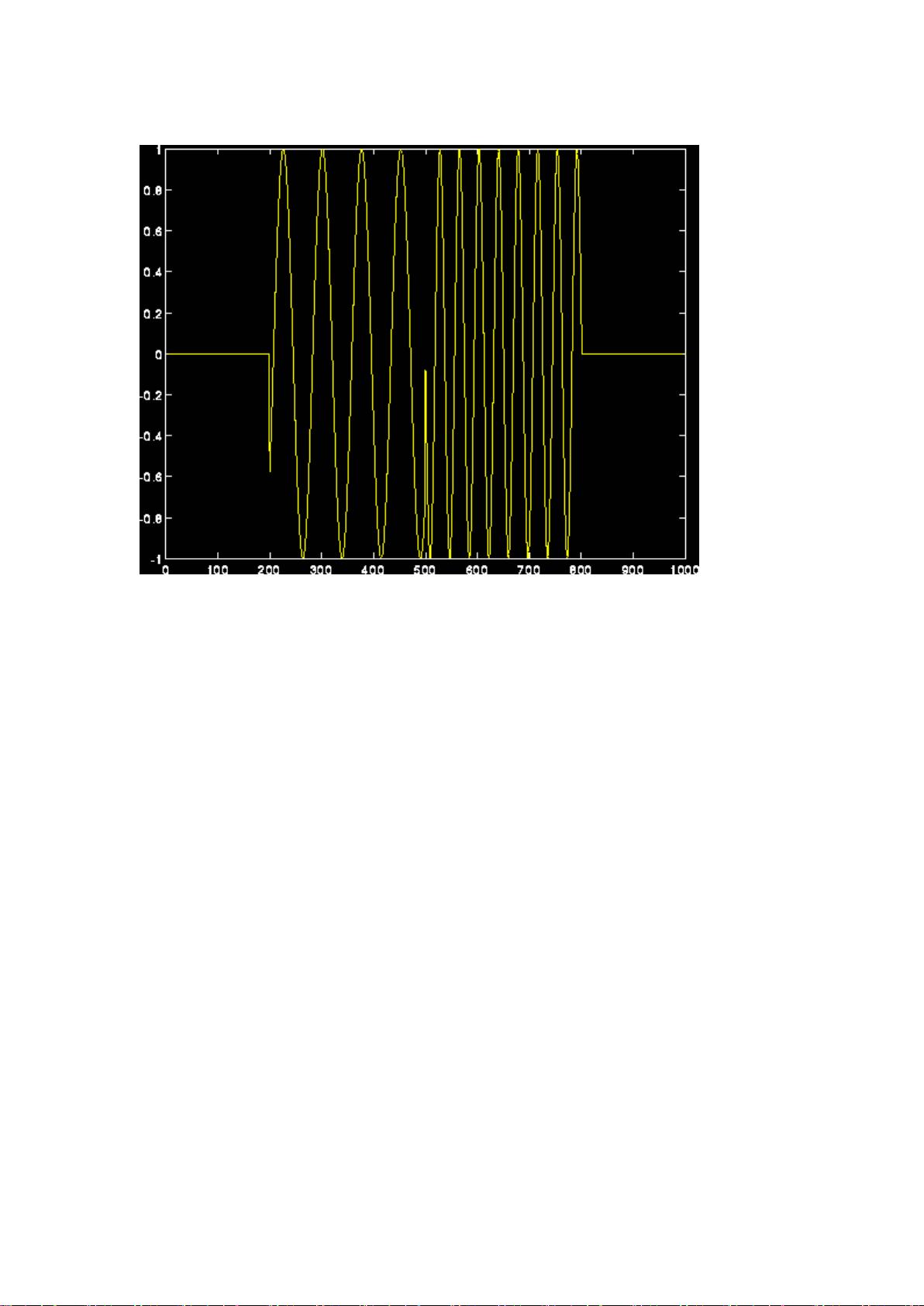
1. **小波变换的引入**:小波变换之所以重要,是因为它能帮助我们解析那些在时域和频域中都有复杂结构的信号。与传统的傅立叶变换相比,小波变换提供了更丰富的信息,因为它可以在不同尺度和位置上分析信号。
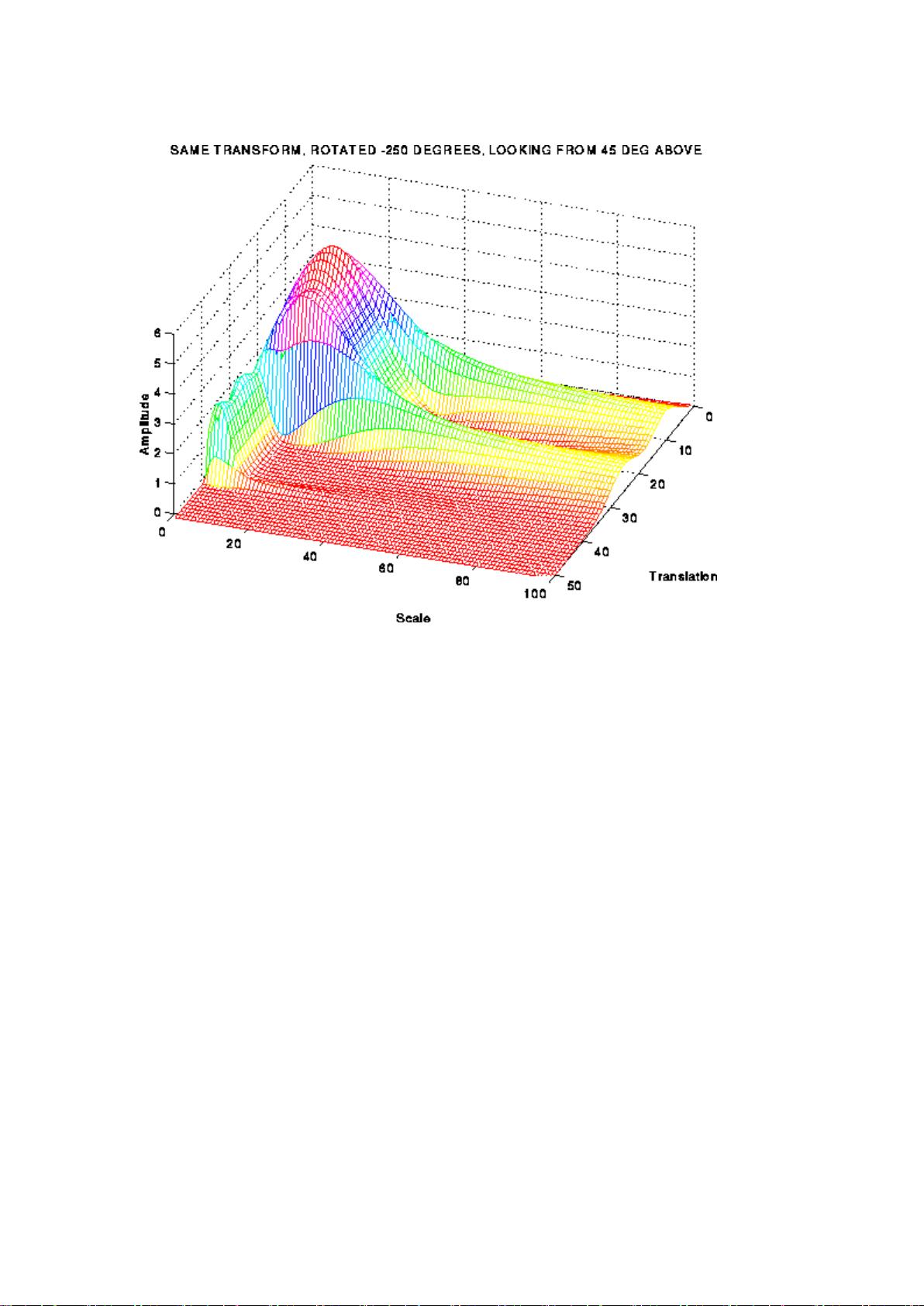
2. **连续小波变换 (CWT)**:小波变换分为连续和离散两种形式。连续小波变换允许我们在任意位置和尺度上应用小波函数,对信号进行细致的分析,适合处理连续的信号数据。
3. **离散小波变换 (DWT)**:离散小波变换则是通过一系列离散的尺度和位置进行分析,更适合数字化的数据。DWT通常用于图像压缩、信号去噪和数据压缩等应用中。
4. **信号变换的目的**:信号变换是为了提取信号中隐藏的信息,尤其是在原始形式中难以察觉的部分。例如,傅立叶变换将信号从时域转换到频域,揭示了信号的频率成分,而小波变换则能在时间和频率上同时提供精细的视图。
5. **小波的优势**:小波变换的一个关键优势是它的时间-频率局部化特性。与傅立叶变换全局分析不同,小波变换可以定位到信号中的瞬态事件或局部特征,这对于检测和分析非平稳信号尤其有用。
6. **教程内容**:教程会逐步讲解小波理论,包括小波函数的构造、小波系数的计算以及如何通过小波分解来处理信号。作者还会讨论不同类型的小波,如Haar小波、Morlet小波等,并展示它们在实际问题中的应用。
7. **适用人群**:无论你是电子工程师、数据科学家还是计算机科学家,只要你对理解和应用小波变换感兴趣,这个教程都会是很好的起点。即使没有深厚的数学基础,也能跟随教程逐步理解小波变换的核心概念。
8. **互动与反馈**:作者鼓励读者在遇到疑问或发现错误时与他联系,以确保教程的准确性和实用性。
通过这篇教程,读者将能够掌握小波变换的基本概念,为进一步研究和应用小波理论打下坚实的基础。无论是信号处理、图像分析还是数据挖掘,小波变换都是一种强大的工具,值得深入学习和探索。
相关推荐







吕东祯
- 粉丝: 0
最新资源
- C#实现程序A的监控启动机制
- Delphi与C#交互加密解密技术实现与源码分析
- 高效财务发票管理软件
- VC6.0编程实现删除磁盘空白文件夹工具
- w5x00-master.zip压缩包解析:W5200/W5500系列Linux驱动程序
- 数字通信经典教材第五版及其答案分享
- Extjs多表头设计与实现技巧
- VBA压缩包子技术未来展望
- 精选多类型导航菜单,总有您钟爱的一款
- 局域网聊天新途径:Android平台UDP技术实现
- 深入浅出神经网络模式识别与实践教程
- Junit测试实例分享:纯Java与SSH框架案例
- jquery xslider插件实现图片的流畅自动及按钮控制滚动
- MVC架构下的图书馆管理系统开发指南
- 里昂理工学院RecruteSup项目:第5年实践与Java技术整合
- iOS 13.2真机调试包使用指南及安装