Matlab绘图与优化：函数最小值与利润最大化决策

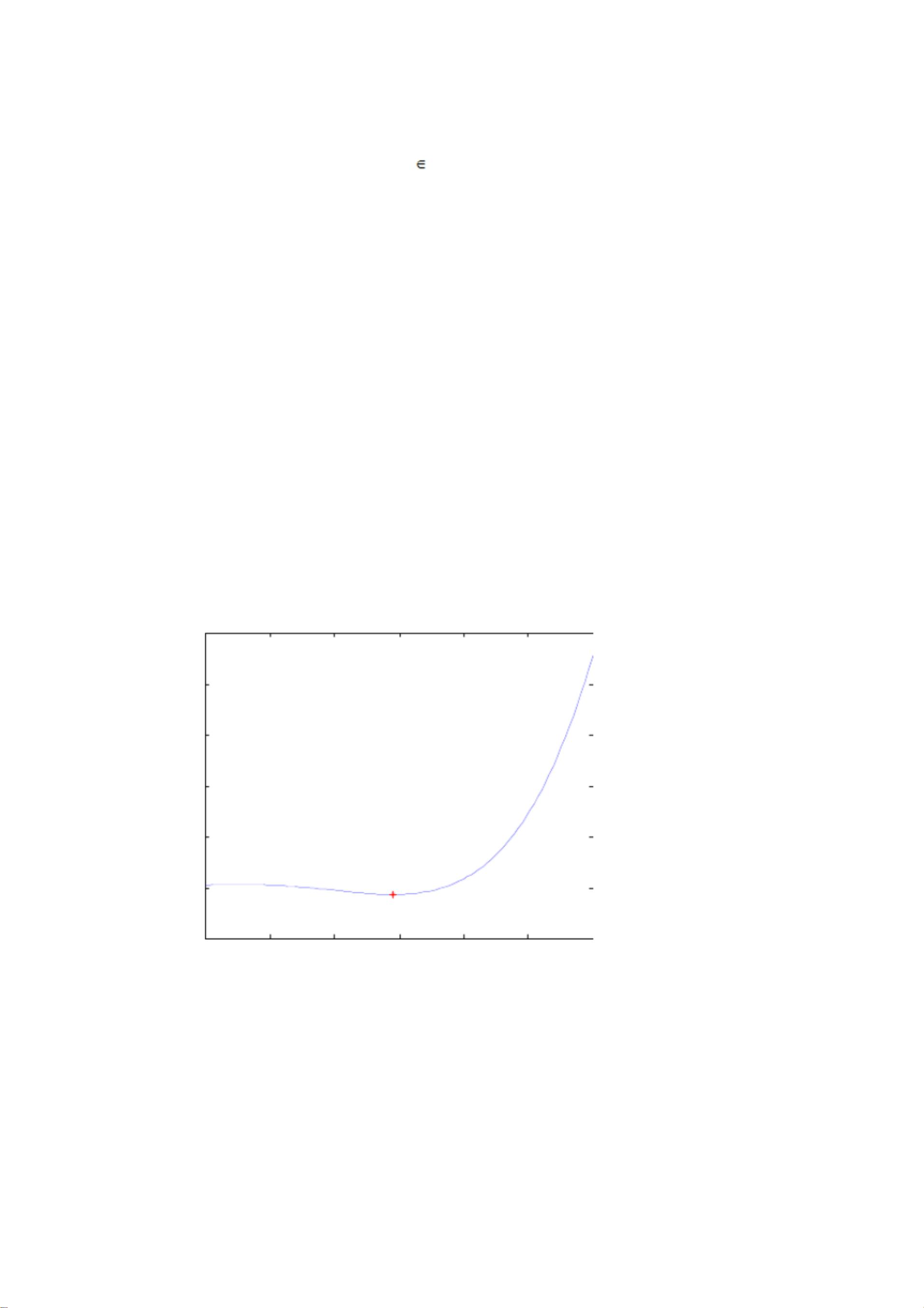
在MATLAB作业题中，学生被要求解决两个相关的问题。首先，他们被要求绘制并分析一个特定函数的图形，即y = x^4 - 4x^3 + 3x + 5在区间[0,6]上的表现。函数图形需包含最小值点，并标注该点的坐标值。通过使用`fminbnd`函数找到最小值点x1=2.9115，对应的最小值y1=-13.1300。代码实现了一个名为`myfun`的函数，用于计算函数值，并结合`plot`和`text`命令展示图形和坐标信息。 第二个问题是关于经济学中的定价策略和广告投入对利润的影响。题目设定的情境是某公司销售彩漆，成本固定为每桶2元。为了最大化利润，需要在考虑产品价格和销量负相关的市场规律下，决定合适的广告费投入和产品售价。给定的数据表明，销售量与价格呈线性关系（表一），而广告费与销售增长因子的关系则呈二次函数（表二）。学生需要建立预期销售量与售价、以及广告费与销售增长因子的数学模型，并据此找出投入最优的广告费和能带来最大利润的售价。 具体建模部分，线性模型假设为销售量y与售价x之间的关系可以用y = 1333.5 - 4222.50 * (1/x)，而销售增长因子与广告费x的关系为二次函数y = 0.409 * x^2 + 0.188 * x + 0.0409。利润p则涉及到售价x和销售增长因子的交互作用，可能涉及一个更复杂的函数，如p = 0.0409 * x^2 + 0.0409 * x * (销售增长因子) + 0.188 * x + 剩余常数项。 通过这些模型，学生需要使用MATLAB的数值优化方法（如`fmincon`或`lsqcurvefit`）来求解利润最大化的条件，找到最佳的广告费和售价组合。这不仅测试了学生的编程技能，也考察了他们在实际商业决策中的经济学理解。 总结来说，MATLAB作业题不仅锻炼了编程基础，还结合了经济学理论，让学生将理论知识应用于实践问题解决中，提升了分析和优化能力。