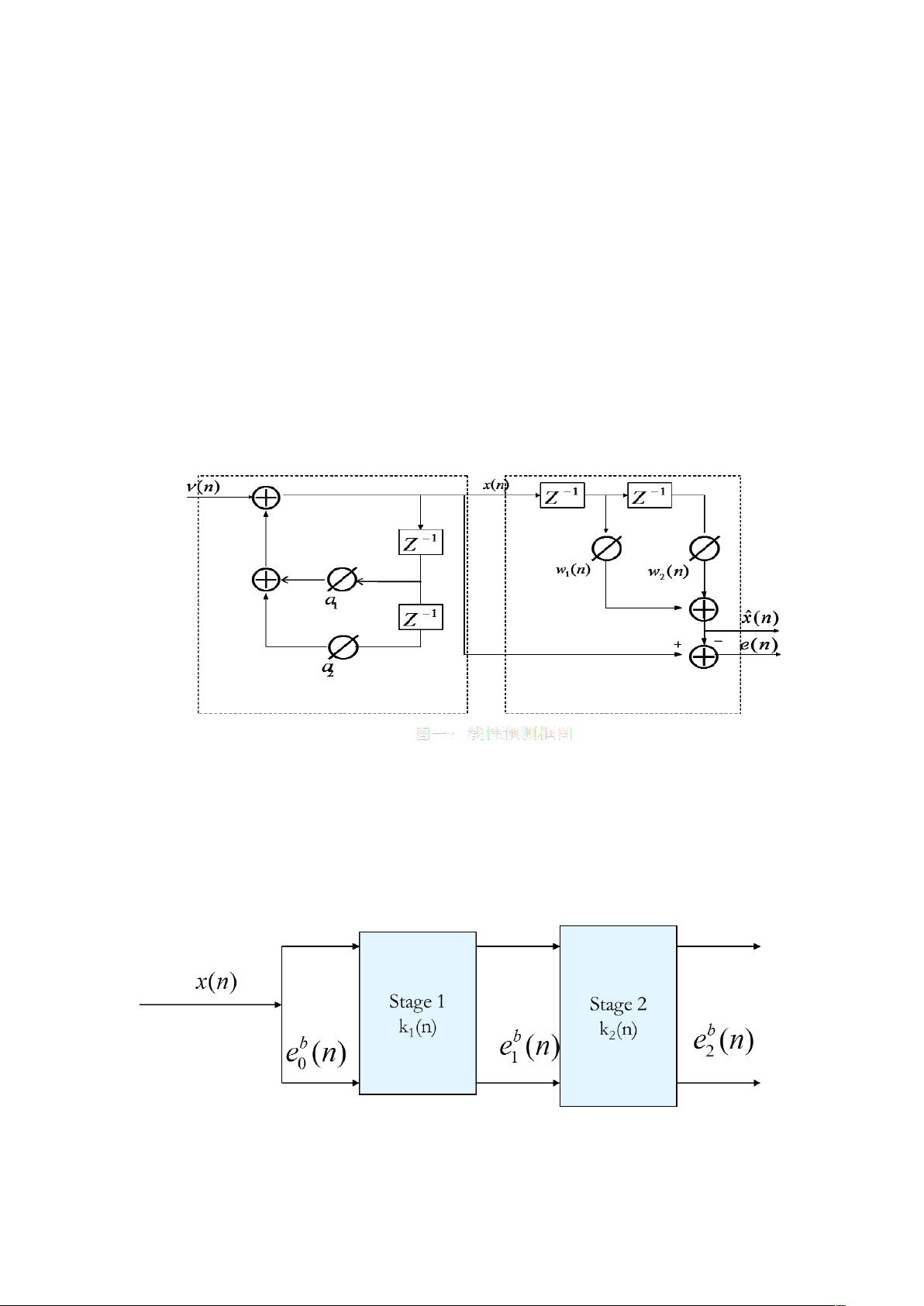
MATLAB仿真实验：格型LMS自适应滤波器及其性能分析

自适应滤波器是一种基于输入和输出信号统计特性动态调整的算法或装置，其目标是优化滤波性能，使得输出信号尽可能接近预期的信号。自适应滤波器既可以应用于连续域，也可以在离散域实现，这里主要关注离散域，其基本结构包括抽头延迟线、可变加权系数和自动调整系数。 在实验设计中，比如名为"自适应信号处理"的实验，MATLAB软件被广泛用于实现格型LMS（Least Mean Square，最小均方误差）算法的仿真。LMS算法是一种常用的自适应滤波器算法，它通过迭代更新滤波器系数，使输出信号的均方误差减小。实验的目的包括： 1. 利用MATLAB中的格型LMS算法来处理信号，掌握其实现细节。 2. 深入研究格型LMS算法的收敛性，将其与横向LMS算法进行比较，理解不同结构对性能的影响。 实验内容涉及实际操作步骤，例如生成高斯白噪声序列，利用二阶自回归模型创建输入信号，并运用z变换。在MATLAB函数gxlms(u)中，关键部分包括信号的递推计算（如x(n)的更新），误差序列(e1f和e1b)的计算，以及滤波器系数(k1和k2)的更新。函数中还包含了学习率参数u，该参数影响算法的收敛速度。 自适应滤波器的设计通常选择FIR（有限 impulse response）结构，因为它避免了IIR（无限 impulse response）滤波器可能遇到的稳定性问题。FIR滤波器的格型结构在自适应滤波器中特别常见，因为它具有良好的性能和稳定性。通过这种方式，实验者能够观察和分析不同滤波器结构在实际应用中的性能表现。 总结来说，自适应滤波器是信号处理中的重要工具，利用MATLAB的格型LMS算法进行实验，不仅可以验证理论知识，还能深入理解自适应算法的工作原理，以及如何根据信号特性调整滤波器以达到最佳效果。实验中对收敛性和算法性能的比较，有助于提高滤波器设计的实际应用能力。