FFT与DFT在信号频谱分析中的应用与影响研究

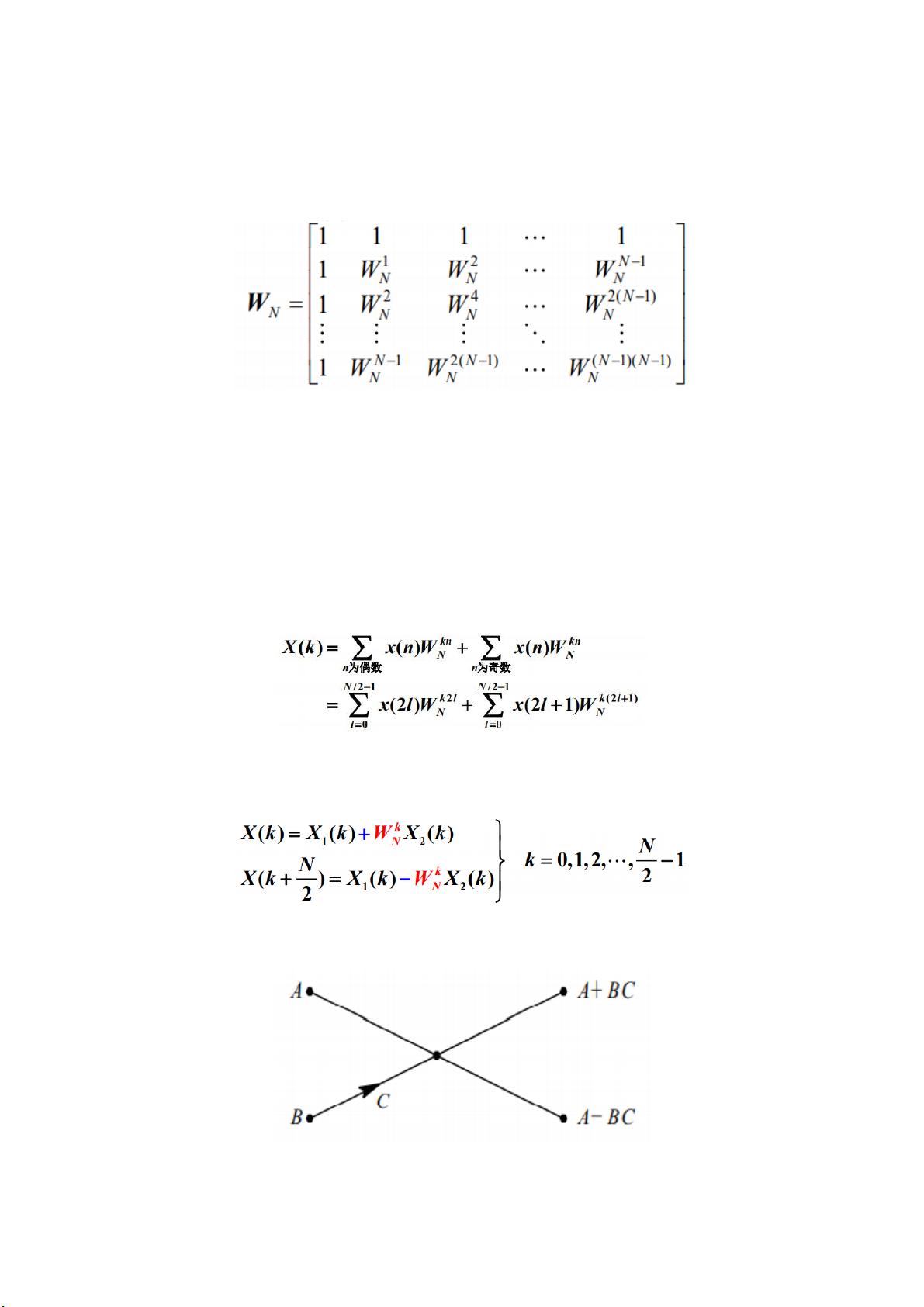
信号的频谱分析是数字信号处理领域中的核心概念，主要利用快速傅里叶变换（FFT）算法进行研究。FFT算法极大地提高了处理效率，本文以计算机程序设计的形式展开实验，其目的是深入了解和应用FFT与离散傅立叶变换（DFT）。 首先，实验步骤涉及生成一系列数字序列，通过计算其离散傅立叶变换（DFT），然后绘制幅频特性曲线和相频特性曲线。这些曲线能直观展示信号在频域的表现，帮助分析信号的频率成分。在离散系统中，实验者会模拟输入序列和单位脉冲响应，通过改变FFT的计算长度，观察其对系统输出响应的影响，探究不同采样点对频谱解析精度的影响。 其次，FFT算法的高效性体现在其对DFT的优化上。DFT原本的计算复杂度为O(N^2)，但FFT利用旋转因子（WNkn = exp(-j * 2πi * Nnk/N)）的周期性、对称性和可约性，将N点DFT分解成多个较短序列的计算，显著降低了计算时间复杂度至O(N log N)。例如，基2时间抽取FFT算法就是通过将时域序列分解为奇偶两个子序列，再运用蝶形运算，进一步减少运算量。 在实验中，选取不同的DFT长度N，观察其对同一序列的频谱计算结果的影响，这体现了信号观测时间和FFT计算长度对频谱分辨率的关键作用。随着N的增加，采样点数增多，频谱分辨率提高，但同时可能带来计算资源的增加。 此外，对于连续时间信号，实验会涉及合适的采样频率，采样后用FFT计算其频谱，探究信号观测时间长度和FFT计算长度对信号频谱分析的实际效果。这不仅涉及信号的离散化过程，还涉及到信号失真和采样定理等问题。 总结来说，本文实验的重点在于理论结合实践，通过编写计算机程序，运用FFT和DFT技术，深入理解信号频谱分析的基本原理和实际应用，以及如何通过调整参数优化频谱计算的效率和精度。这些知识点对于数字信号处理工程师、研究人员和学生来说，都是至关重要的基础知识。