ECC教程：理解并应用椭圆曲线加密技术

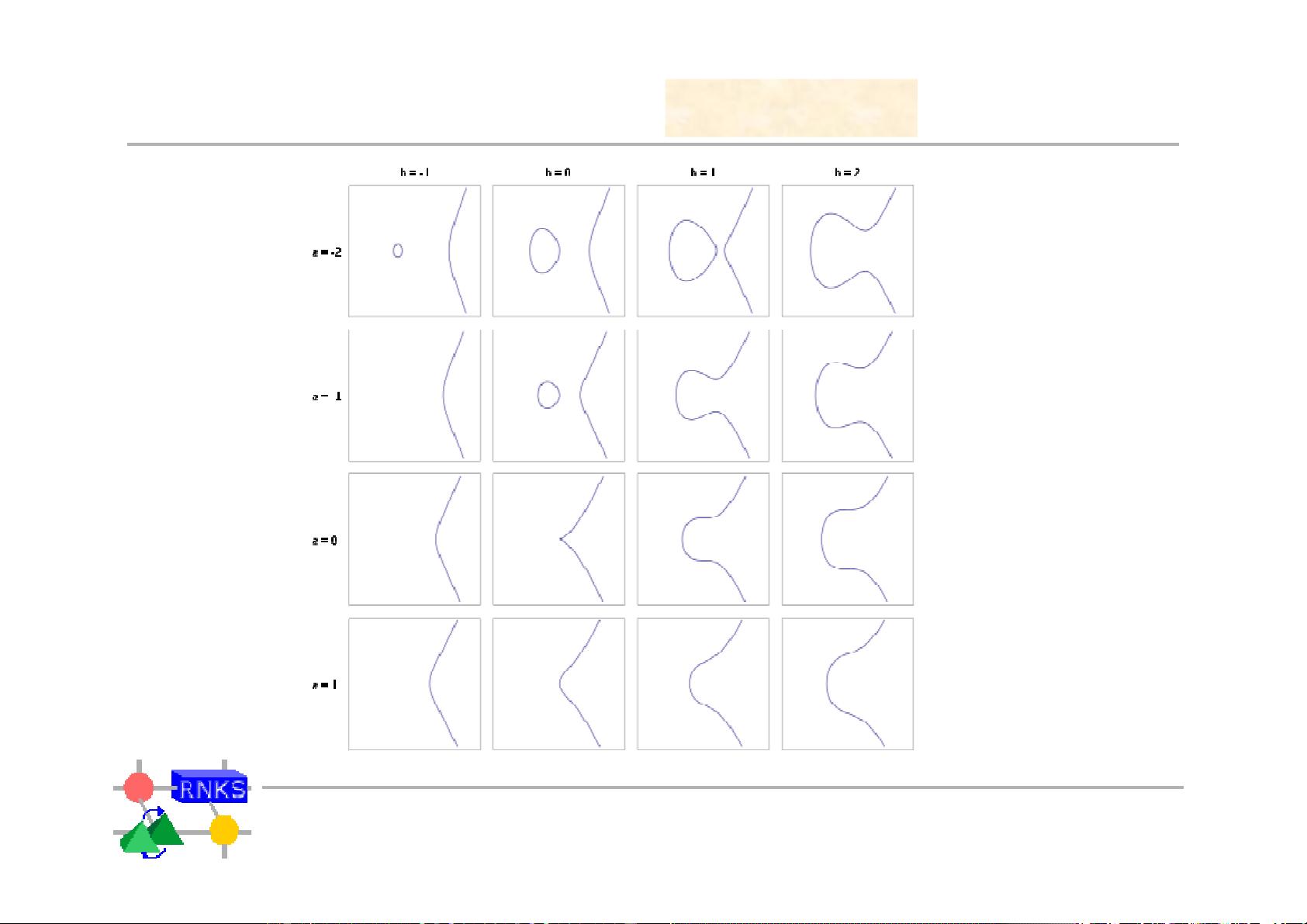
本篇教程旨在解析椭圆曲线密码学（Elliptic Curve Cryptography, ECC）的概念和应用，由Brandenburg Technical University of Cottbus的Computer Networking Group提供，作者 Fuwen Liu（lfw@informatik.tu-cottbus.de）撰写了关于ECC的深入教程。教程分为七个部分，帮助读者逐步理解： **I. Introduction** 首先，引入了加密技术的基础，解释了其目的，包括确保信息在公开渠道的安全传输，目标是保护隐私，防止未经授权访问，以及验证通信双方的身份。加密系统被分为两类：无条件安全系统和可实现安全系统，其中一次性密码本（One-time pad）是典型的无条件安全示例。 **II. Elliptic Curves over Real Numbers** 这一部分探讨了椭圆曲线在实数域上的性质，可能涉及曲线的定义、参数选择以及它们在加密中的作用，因为实数域下的椭圆曲线提供了不同的数学特性，有助于设计高效且安全的加密算法。 **III. Elliptic Curves over Prime Field and Binary Field** 接下来的部分重点关注在素数域（如GF(p)）和二进制域（如GF(2^n））上的椭圆曲线，这是ECC中最常用的设置，因为这些有限域提供了更简单的计算和更快的处理速度，对于现代密码学应用至关重要。 **IV. Security Strength of ECC System** 这部分分析了ECC系统的安全性，讨论了为什么尽管基于比传统公钥密码系统（如RSA）更短的密钥，ECC仍能提供相当的安全级别，这是因为椭圆曲线的离散对数问题（Discrete Logarithm Problem, DLP）被认为在大整数域上是困难的。 **V. ECC Protocols** 随后介绍了实际应用中的ECC协议，如Diffie-Hellman密钥交换协议（ECDH）和ElGamal公钥加密，这些协议利用椭圆曲线的性质来保证通信的保密性和完整性。 **VI. Patents and Standards** 在专利与标准方面，章节探讨了ECC在专利保护下的发展状况，以及它如何成为国际标准（如FIPS 186和SECG）的一部分，这些标准化过程确保了ECC在全球范围内的一致性和接受度。 **VII. Final Remarks** 最后，作者总结了教程的主要要点，可能提到ECC在当前信息安全领域的优势、挑战及未来发展方向，鼓励读者继续探索这一不断发展的领域。 通过阅读这篇教程，学习者能够深入了解椭圆曲线密码学的基本概念、其实现细节及其在实际安全措施中的应用，有助于提升对现代加密技术的理解和实践能力。