Python实现LDA线性判别分析的MATLAB风格指南

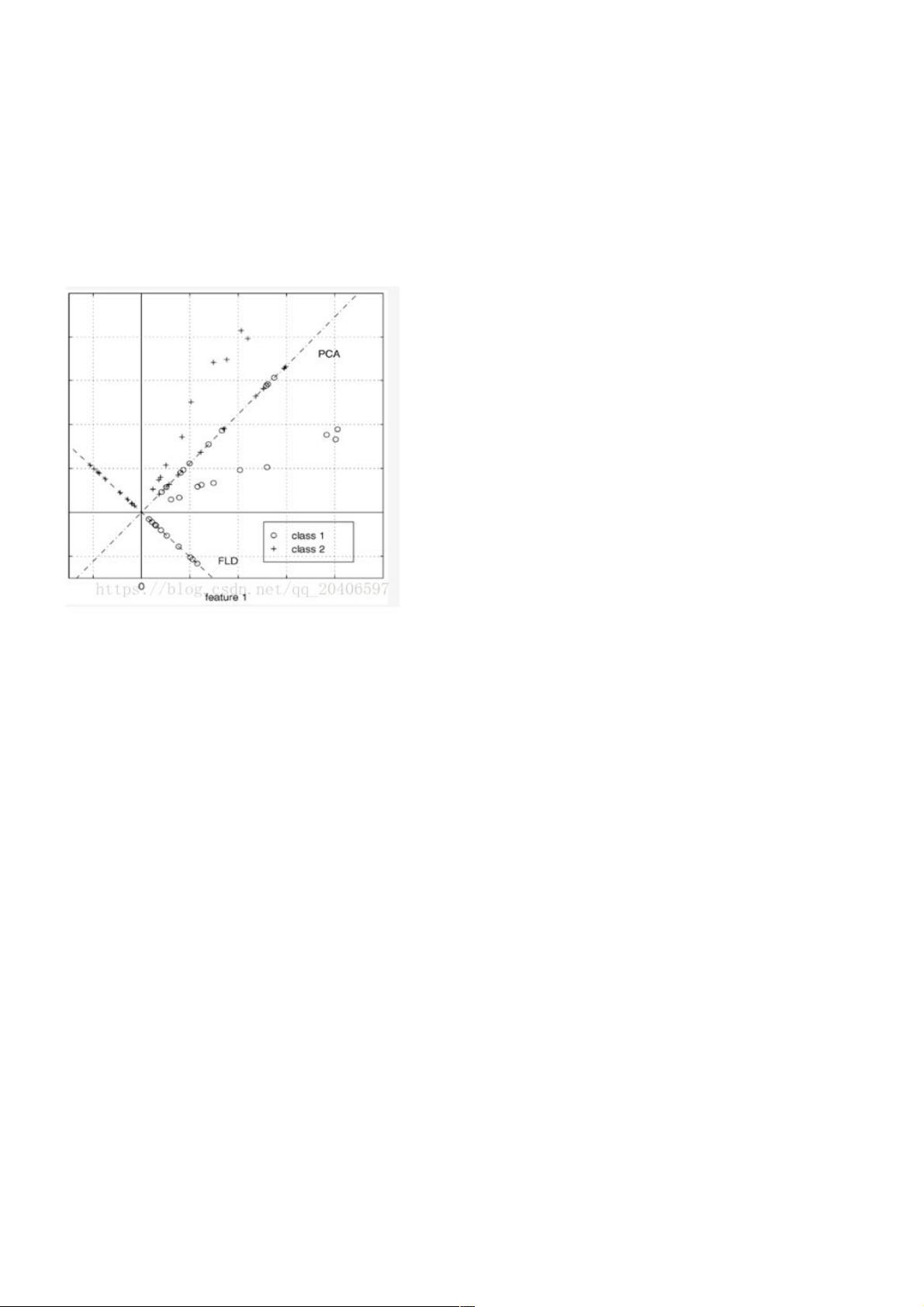
"Python实现线性判别分析(LDA)的MATLAB方式" 线性判别分析（LDA）是一种统计学方法，常用于多类别的分类任务，尤其在高维数据降维时表现出色。LDA的核心思想是寻找一个线性变换，将原始数据投影到一个低维空间中，使得不同类别的样本间距离最大化，同时保持同一类别内部的样本距离最小化，从而提高分类的准确性。这种方法与主成分分析（PCA）不同，PCA主要是为了无损地保留数据信息，而LDA则考虑了类别信息，是监督学习的一种降维手段。 LDA的关键步骤包括： 1. 计算类别内样本协方差矩阵（$S_w$）和总样本协方差矩阵（$S_b$）。类别内协方差矩阵是每个类别样本的协方差矩阵的加权平均，总样本协方差矩阵则是所有样本的协方差矩阵。 2. 针对监督学习的特性，LDA的目标是最大化类间距离（即$S_b$）和最小化类内距离（即$S_w$）。通过Fisher判别准则，我们寻求最大化以下比例： $$\frac{|\text{det}(S_b)|}{|\text{det}(S_w)|}$$ 这等价于求解矩阵$S_w^{-1}S_b$的特征值和特征向量。最大的特征值对应的特征向量决定了最佳的投影方向，这将使类别间的区分度最大。 3. 最优的投影方向W是矩阵$S_w^{-1}S_b$的最大特征值对应的特征向量。通常，我们可以选择不超过类别数减一（C-1）的最优特征向量作为投影轴，因为这些特征向量将数据投影到一个低维空间，保持最大的类间距离。 4. 投影数据：计算每个样本在这些特征向量上的投影点，得到低维表示的新数据。这可以通过矩阵乘法实现，即将原始数据乘以投影矩阵W。 在MATLAB中实现LDA，首先需要准备训练数据集，然后按照上述步骤进行计算。代码通常包括数据预处理、计算协方差矩阵、求解特征值和特征向量，以及投影数据到新空间。MATLAB的`eig`函数可以用来计算特征值和特征向量，而数据的投影则可以用矩阵乘法完成。 LDA在机器学习和数据分析领域广泛应用，特别是在文本分类、人脸识别和高维数据预处理中。通过合理地运用LDA，可以有效地降低数据的复杂性，提升模型的分类性能。