树型动态规划在信息学竞赛中的应用

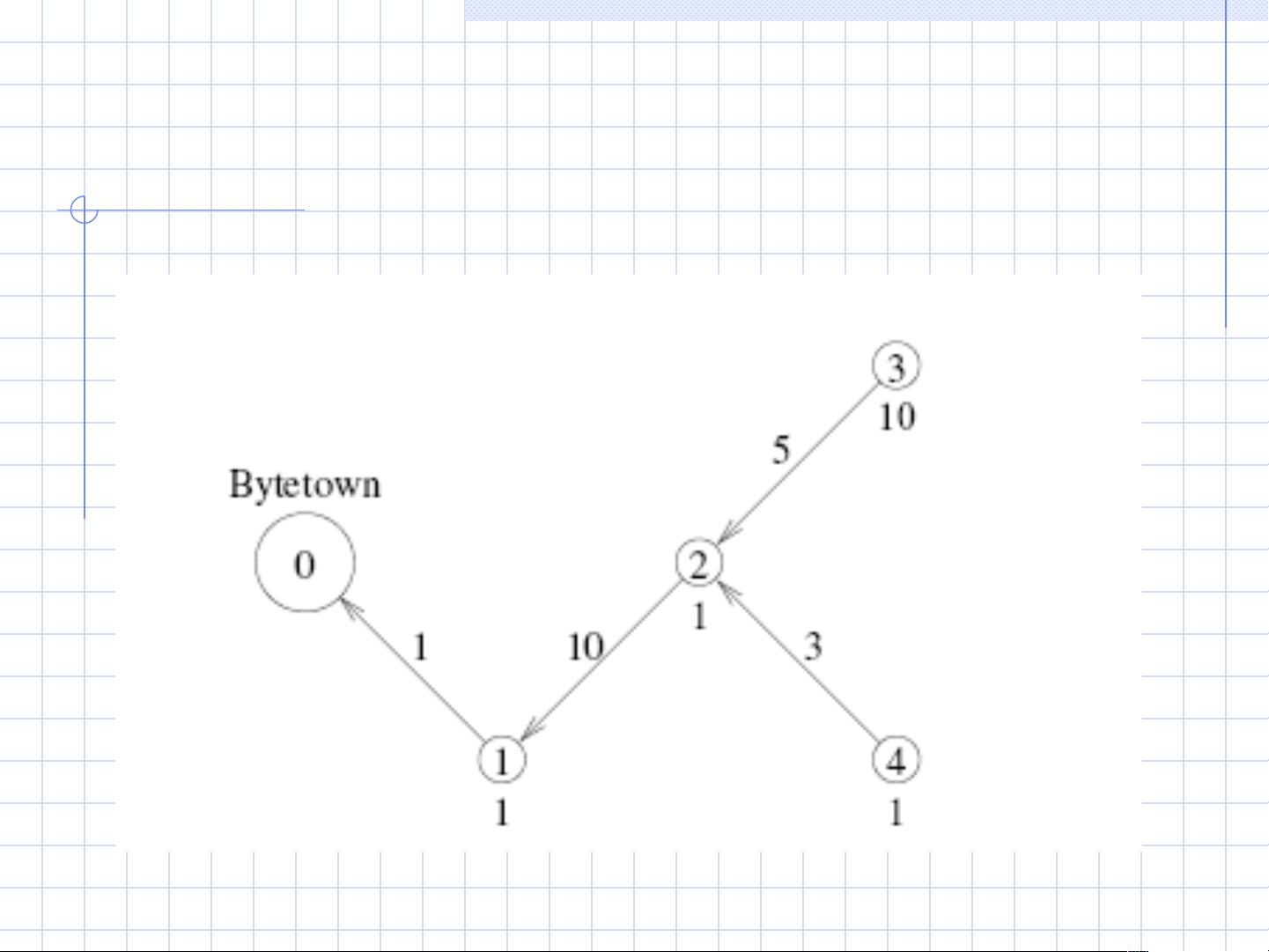
"陈瑜希《多角度思考 创造性思维》.ppt" 这篇文档主要由江苏省南京外国语学校的陈瑜希分享，主题聚焦于多角度思考和创造性思维在解决复杂问题，特别是信息学竞赛中的应用。文档特别关注树型动态规划这一策略，它是解决大规模、最优性问题的有效方法，特别是在面对树结构数据时，传统的枚举和贪心算法往往力有不逮。 在信息学竞赛中，树型动态规划问题日益常见，它们往往经过巧妙设计，融合多种算法思想，对参赛者的分析能力和创新思维提出高要求。陈瑜希通过分析国际和全国比赛中的实例，如NOI03的"逃学的小孩"、IOI05的"河流"、NOI06的"网络收费"以及POI04的"山洞"等，揭示了解决这类问题的关键思路。 以"河流"问题为例，设定有n个伐木村庄，木材需从各个村庄运输至0号节点的伐木场，目标是在不超过k个村庄建立额外的伐木场以最小化运输成本。每个村庄沿着河流只有一条路径通往0号节点。问题的核心在于构建合适的动态规划状态和转移方程。 状态的确立是动态规划的基础，对于这个问题，我们需要知道以某个节点为根的子树中建立了多少个伐木场，但仅此还不够，还需要包含伐木场的具体位置信息。为此，我们可以定义状态`f[kleft][to][from]`，表示在以`from`为根的子树中建立了`kleft`个伐木场，且最近的祖先伐木场位于`to`时的最低总费用。这里的`to`不一定是`from`的最近祖先，而是任意祖先，这样的设计是为了便于状态转移。 状态的转移是动态规划的核心部分，通常涉及递归或迭代的过程。在这个问题中，我们需要考虑如何从子问题的状态推导出原问题的状态。通过逐步构建并优化状态转移方程，可以找到最优解，即最小的运输费用。 陈瑜希的报告强调，解决这类问题不仅仅在于掌握解题技巧，更重要的是培养多角度思考和创造性思维，这包括深入理解问题本质、灵活运用算法、以及在面对复杂情况时的创新能力。这种思维方式不仅在信息学竞赛中至关重要，也是在日常工作中解决复杂问题的关键能力。