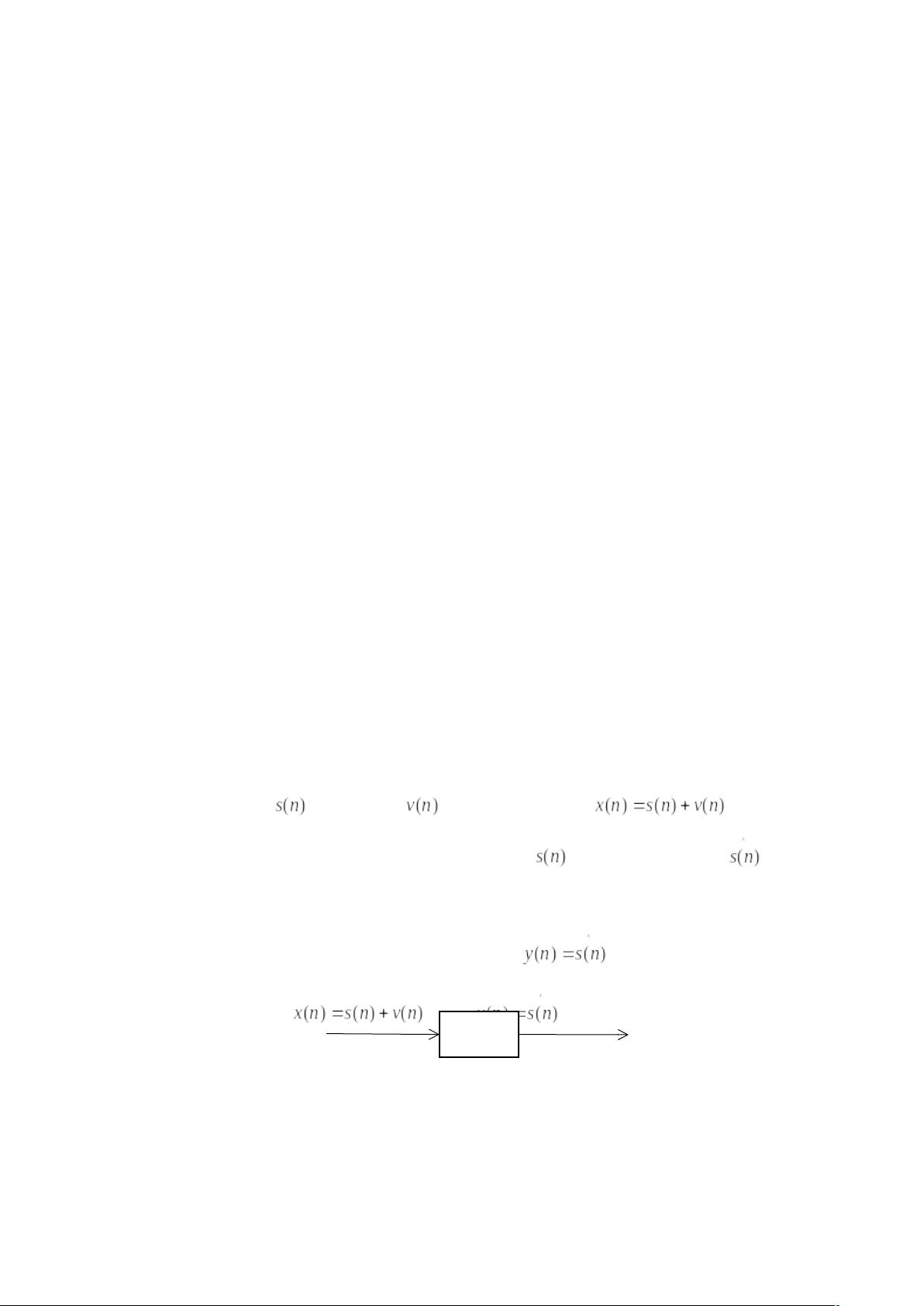
MATLAB下维纳滤波去噪：chirp信号在不同噪声环境下的信号恢复

维纳滤波是一种在信号处理领域广泛应用的技术，尤其在噪声环境下恢复信号。本文主要关注于如何利用维纳滤波器从含有高斯白噪声的chirp信号中提取出原始信号。chirp信号，一种随时间频率变化的信号，常常被用于模拟鸟类叫声等自然信号。实验中，chirp信号被叠加了不同强度的高斯白噪声，形成观测信号。白噪声具有各频率成分的功率均匀分布，使得信号识别变得困难。 维纳滤波的原理基于均方误差最小化，目标是找到一个线性滤波器，使得通过滤波器后的信号与原始信号之间的误差最小。该滤波器的设计需要满足正交性原则，即滤波器应该消除与信号无关的噪声部分。维纳—霍夫方程是求解这一问题的关键，它在时域和频域中都有相应的表达形式。在时域中，通常采用递推或逼近方法求解，通过自相关矩阵和互相关矩阵来计算最优的冲击响应。而在频域中，由于维纳—霍夫方程的特性，可能需要借助于z变换和白化技术来解决。 在MATLAB环境中，作者首先创建了一个chirp信号和高斯白噪声的混合观测信号，然后编写了维纳滤波的程序，包括信号的滤波、波形绘制以及信号的播放，以便通过听觉判断滤波效果。实验结果显示，当信噪比为20时，维纳滤波器能够有效地去除噪声，使重构的chirp信号接近原始信号，证明了设计滤波器的有效性。 通过这个过程，读者可以了解到维纳滤波的实际应用步骤，从信号模型建立到滤波器参数的求解，再到结果验证，全面展示了信号处理中一项关键技术的实施细节。这不仅有助于理解和掌握维纳滤波理论，也为其他类似噪声抑制问题提供了实用的解决方案。