PCA模型实验报告：沈子鸣-1170301007

"PCA模型实验报告，由沈子鸣完成，涵盖了PCA算法的原理和实现，包括人工数据生成和人脸数据压缩的应用。实验环境为Windows10，Python3.7.4，Jupyter Notebook6.0.1。" PCA（主成分分析，Principal Component Analysis）是一种常用的数据分析方法，它通过线性变换将原始数据转换到一个新的坐标系统中，使得新的坐标系的第一轴（主成分）是原数据方差最大的方向，第二轴是除第一轴外方差最大的方向，以此类推。PCA的主要目标是降低数据的维度，同时尽可能保留数据的大部分信息，常用于数据压缩和可视化。 PCA算法的实现分为以下几个步骤： 1. **数据预处理**：首先，计算数据集的均值，然后对每个样本减去该均值，实现数据的中心化，这是为了消除各特征之间的尺度差异，确保每个特征对PCA的影响平等。 2. **计算协方差矩阵**：在数据中心化之后，构建协方差矩阵。协方差矩阵反映了各个特征之间的关联程度，它的对角元素表示单个特征的方差，非对角元素表示特征间的协方差。 3. **特征值分解**：对协方差矩阵进行特征值分解，得到一组特征值和对应的特征向量。特征值代表了主成分的重要性，特征向量则指示了主成分的方向。 4. **选择主成分**：选取具有最大特征值的特征向量，这些向量对应了数据的主要变化方向，也就是主成分。通常，选取前k个最大特征值对应的特征向量，其中k是目标降维后的维度。 5. **投影数据**：将中心化后的数据乘以这k个特征向量构成的矩阵，完成数据的降维。这个新坐标系下的数据就是降维后的数据，包含了原始数据的主要信息。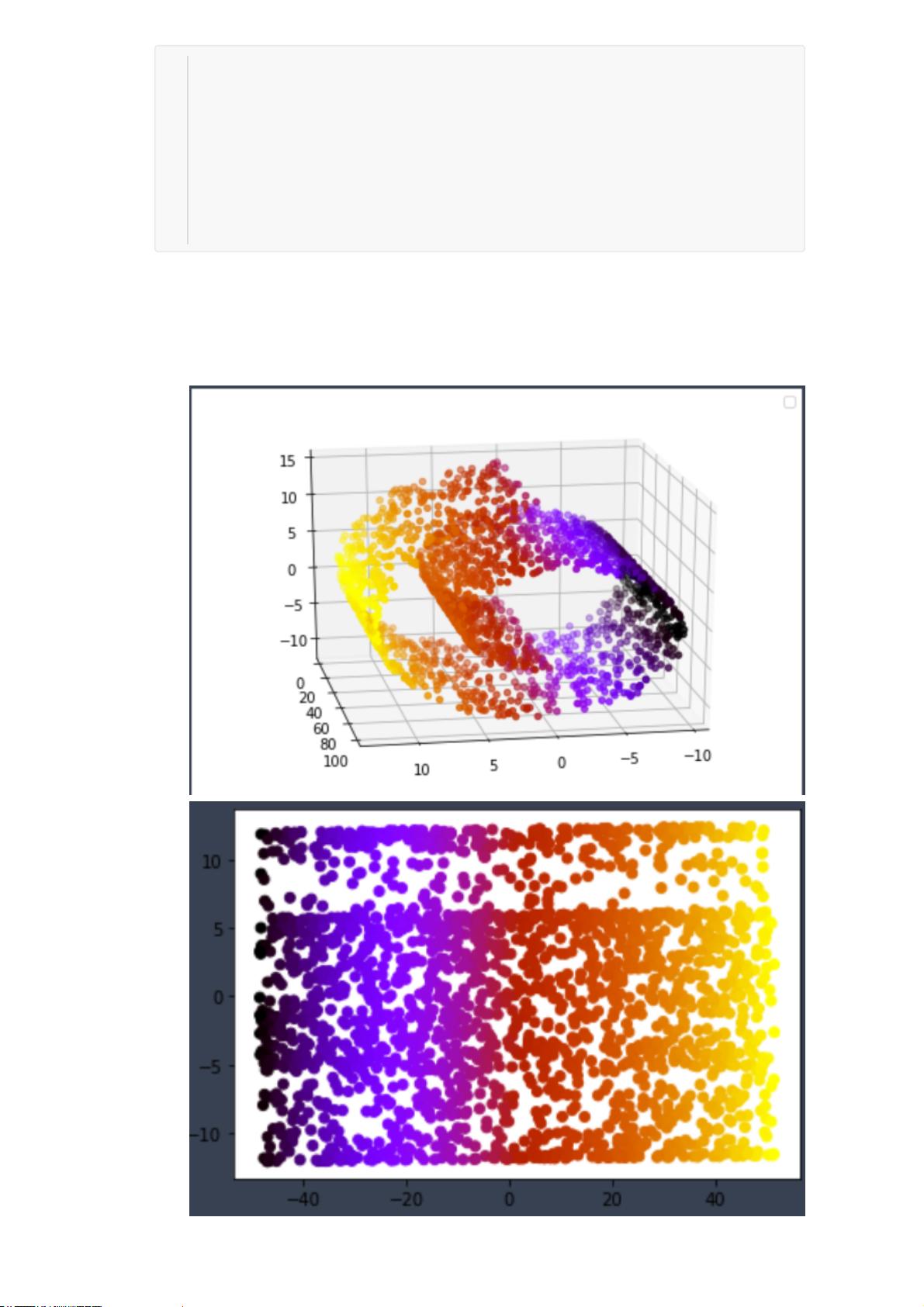 在实验中，沈子鸣首先人工生成了一组三维数据，模拟了数据主要分布在低维空间的情况，然后使用PCA进行主成分提取。接着，他应用PCA方法处理人脸数据，通过降维找到人脸的主要特征，并利用这些特征对人脸图像进行重构，通过比较重构图像与原始图像的信噪比来评估PCA的效果。 PCA在人脸数据压缩中的应用，可以显著减少存储和处理图像所需的空间和时间，同时保持图像的关键信息。这种降维方法在人脸识别、图像压缩、高维数据可视化等多个领域都有广泛应用。通过PCA，复杂的数据集可以变得更加易于理解和处理。