kNN算法详解：优缺点与改进策略

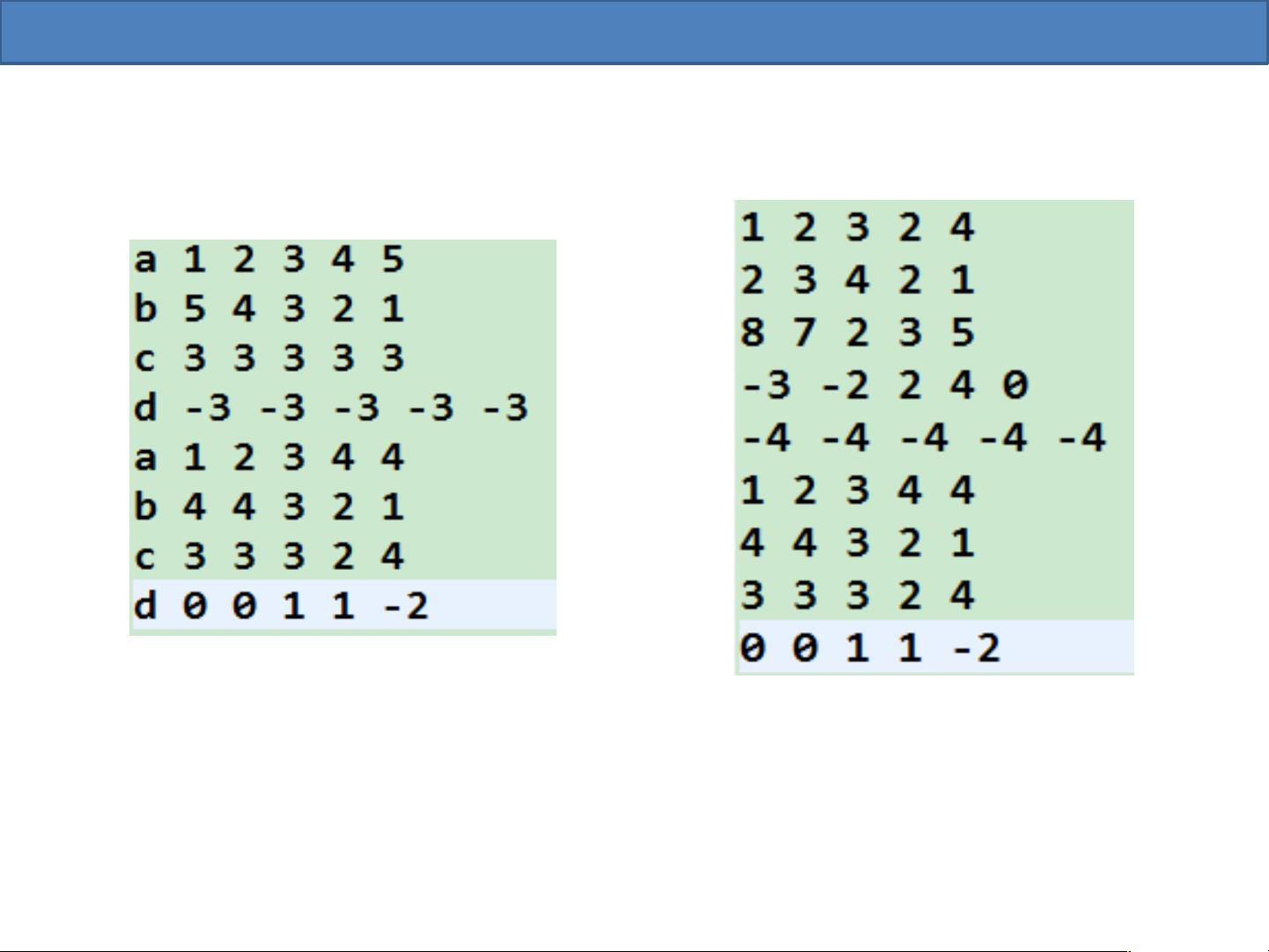
"kNN算法是数据挖掘中的一种基础分类方法，全称为k-最近邻算法。该算法基于实例的学习，通过寻找与新样本最接近的k个已知类别的样本，根据这k个样本的类别分布来决定新样本的类别。" kNN算法的核心思想是假设新的数据点将与训练集中最相似的k个数据点具有相同的类别。这里的k是一个正整数，通常由用户预先设定。算法的流程包括以下几个步骤： 1. 计算新样本点与所有训练样本之间的距离。最常用的距离度量是欧氏距离，但也可以使用其他距离度量，如曼哈顿距离、切比雪夫距离等。 2. 根据预设的k值，选取与新样本点距离最近的k个训练样本。 3. 对这k个样本的类别进行统计，选择出现次数最多的类别作为新样本的预测类别。在某些情况下，可能会使用加权投票，距离更近的样本权重更大。 kNN算法的优点包括： - 实现简单，理解直观，不需要训练阶段，只需在预测时执行。 - 对异常值和噪声有一定的容忍度，因为它们可能只影响少数邻居。 - 不受样本数量不平衡的影响，分类决策主要依赖于最近的邻居。 - 特征选择的影响相对较小，有助于减少错误项。 然而，kNN算法也存在明显的缺点： - 计算量大，特别是在高维空间中，由于“维度灾难”导致的计算复杂度增加。 - k值的选择对结果有很大影响，过小可能导致过拟合，过大可能导致噪声引入。 - 使用欧氏距离可能导致“长尾效应”，即某些特征差异大的样本被错误地认为很近。 - 对于大规模数据集，存储和搜索最近邻可能成为瓶颈。 为了改进kNN算法，可以考虑以下策略： - 调整k值：选择合适的k值，通常通过交叉验证来确定。 - 类别判定策略：除了多数投票，还可以使用加权投票，或者考虑样本的密度。 - 距离度量：使用加权距离，如考虑特征的重要性，或者使用更复杂的距离度量，如余弦相似度、马氏距离等。 - 算法优化：采用kd树、球树等数据结构加速最近邻搜索，或者使用降维技术（如主成分分析PCA）降低计算复杂性。 - 频率方法：利用样本出现的频率来调整距离，例如VDM（值差异度量）。 kNN算法是一种强大的非参数分类工具，但需要谨慎处理其固有的问题，以获得更准确和高效的分类结果。在实际应用中，结合领域知识和数据特性，对算法进行适当的优化和调整是至关重要的。