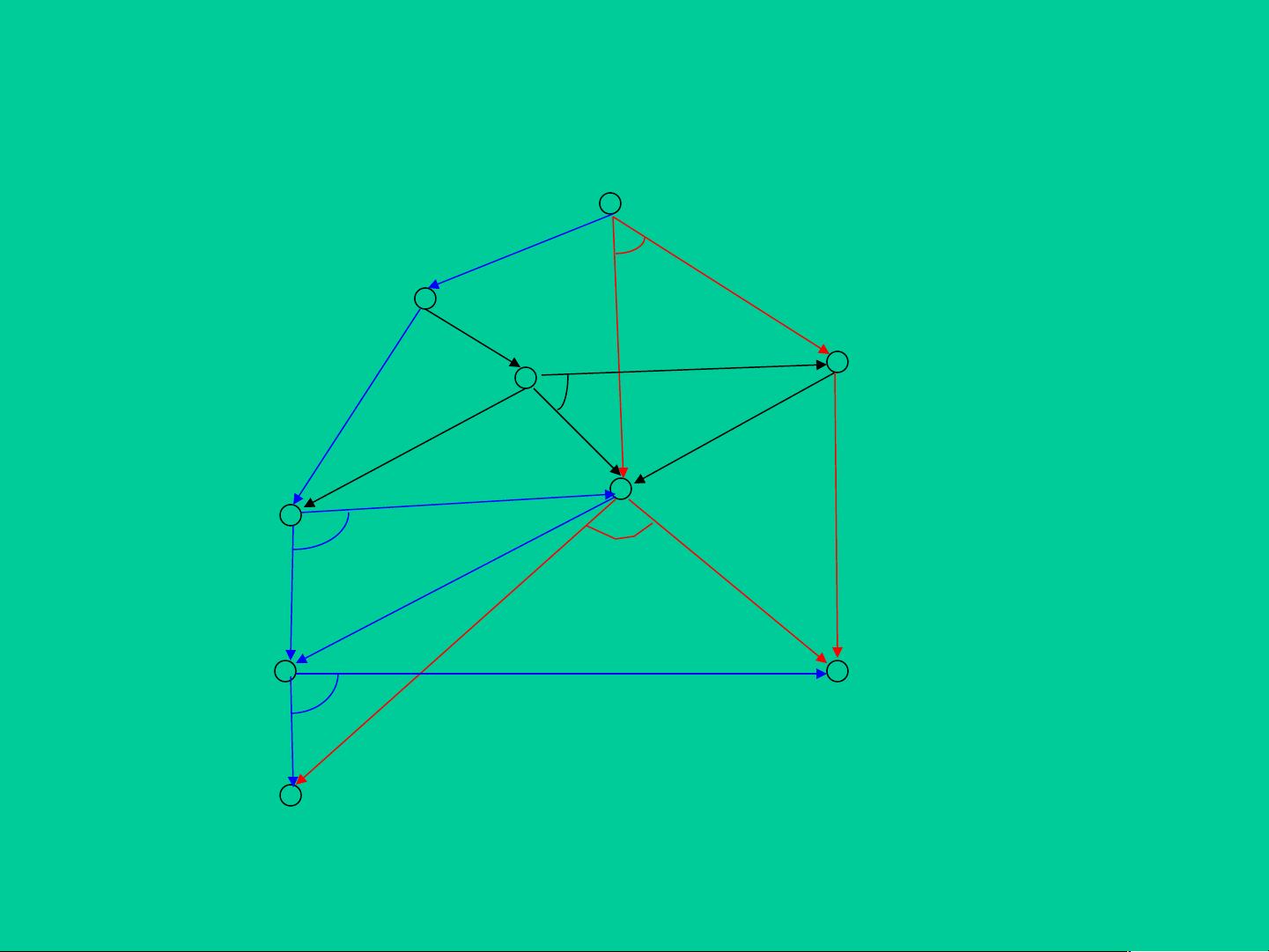
与或图搜索在人工智能中的应用解析
版权申诉
PPT格式 | 378KB |
更新于2024-07-02
| 155 浏览量 | 举报
"这份资料主要讲述了人工智能领域中的与或图搜索方法,用于解决复杂问题的归约策略。通过将大问题分解为子问题,利用与或图这一图形结构来表示问题的分解过程。与节点表示所有子问题必须都有解,父问题才会有解;而或节点则表示只要其中一个子问题有解,父问题就有解。在与或图中,搜索的目标不是找到目标节点,而是构建一个解图,证明初始节点存在解。解图的定义涉及从某个节点到目标节点集合的路径条件。此外,搜索过程中还会涉及到耗散值的计算,这是评估和选择搜索路径的重要依据。"
在人工智能中,与或图搜索是一种高效的问题解决策略,特别适合处理复杂的问题空间。问题归约法是这种方法的基础,它通过将复杂问题逐步分解为更小的、可以直接解答的子问题,直至达到本原问题,即可以直接得出答案的问题。这一过程可以通过与或图清晰地表示出来。
与或图是由与节点和或节点组成的图形结构。与节点表示一个节点的解依赖于其所有子节点的解,只有当所有子节点都有解时,该节点才有解。相反,或节点表示多个子问题中的任何一个有解,都能导致父问题有解。这种结构有助于表示问题的不同解路径和组合可能性。
在与或图中,K-连接符用于表示一个节点通过一个算符归约出的多个子问题,每个子问题都是一个独立的后继节点集合。解图是搜索过程的核心,它是一个从初始节点到目标节点集合的子图,证明了初始问题有解。解图的构造遵循特定规则,包括从单个节点到解图,以及从连接符到子解图的递归定义。
在实际搜索过程中,不仅需要找到解图,还需要计算和考虑每个节点的耗散值,这通常与解决问题的成本或效率有关。耗散值的计算有助于指导搜索算法选择最优路径,以尽可能有效地找到问题的解决方案。
总结来说,与或图搜索是一种在复杂问题空间中寻找解决方案的有效工具,通过问题归约、与或图的构建和解图的搜索,以及耗散值的计算,能够系统性地解决多分支、多路径的问题。这种方法在人工智能和计算机科学的许多领域,如路径规划、游戏AI和决策制定等,都有着广泛的应用。
相关推荐








智慧安全方案
- 粉丝: 3861
最新资源
- Wenyu Zhao的个人技术网站构建指南
- DBSync V1.9:实现数据库实时同步与异构兼容
- C++实现的学生信息管理系统的增删改查功能
- 美团点评2018技术年货盘点(上)
- 多功能JS下拉列表,支持搜索和样式定制
- 安卓图标设计精选集:开发者必备图标大全
- Linux环境下自动化分发Windows OVA实例教程
- Play框架Scala编译时依赖注入示例项目分析
- 安卓CWM.ZIP自定义刷机包压缩文件解压缩指南
- Win64OpenSSL安装与环境变量配置指南
- 掌握键盘快捷操作:typing-cheatsheets快捷键指南
- Go开发的分布式内存 MMO 游戏服务器架构设计
- Delphi字符串分割方法及示例源码解析
- FPGA实现经典俄罗斯方块游戏教程
- QtCustomControls:实用的自定义控件库
- 深入剖析J2EE经典实例及其应用