Mathematical Problems in Engineering
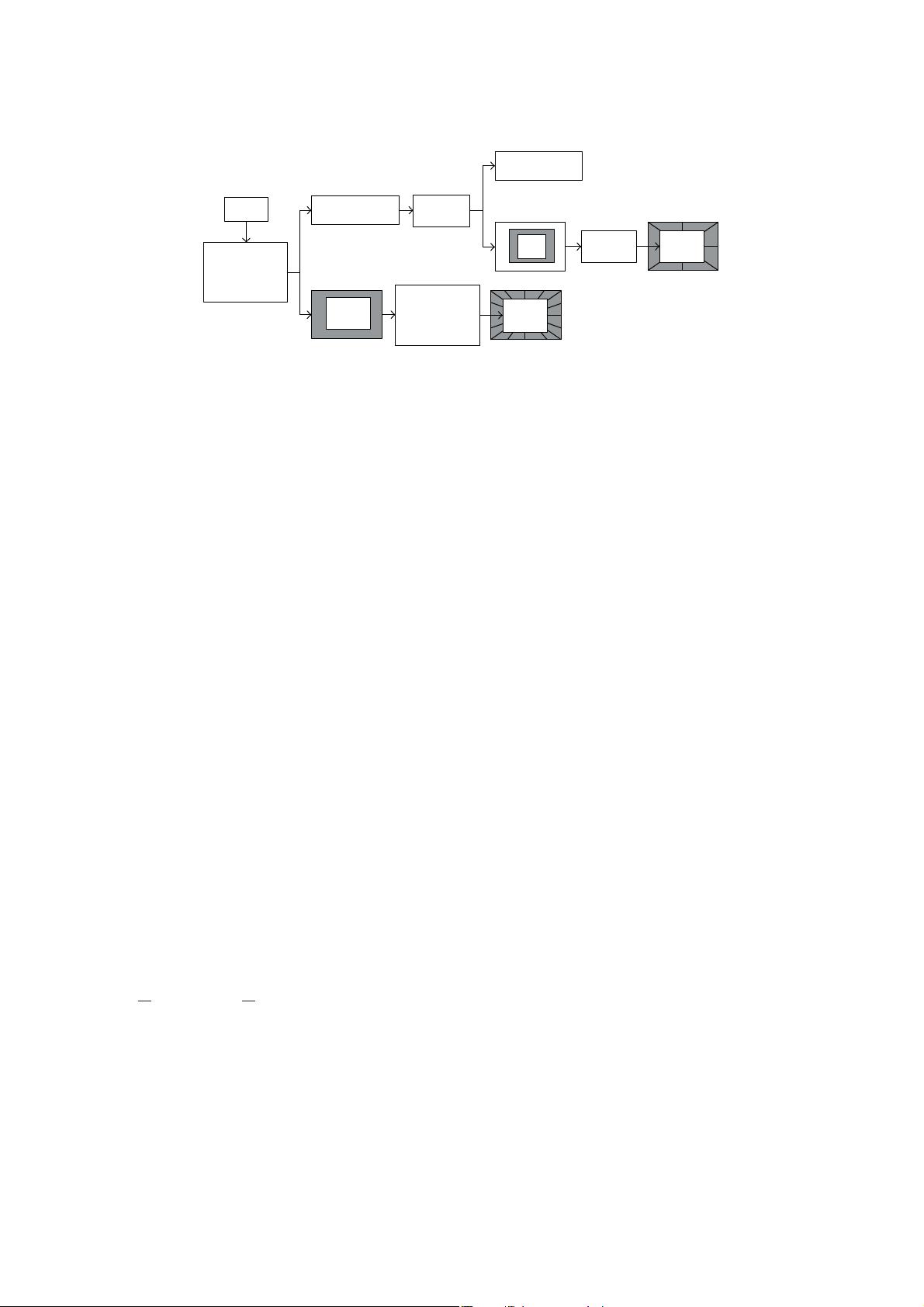
Image
Nonsubsampled
Nonsubsampled
pyramid lter
bank
directional lter
bank
(NSPFB)
(NSDFB)
Low frequency
Low frequency
image
image
image
Bandpass
Bandpass
image
NSPFB
NSDFB
High frequency
directional subband
images
High frequency
directional subband
images
F : NSCT ow graph.
contourlet transformation, the lters of NSCT have better
frequency selectivity and regularity, which can better perform
subband direction decomposition. In contrast to wavelet
decomposition, NSCT is a multiscale, multiresolution, and
multidirectional analysis method. Because of the exibility
of the direction decomposition achievable using NSCT, more
detailed information about the image can be obtained during
the image decomposition process. e resulting transform
not only has the multiscale and time-frequency-localisation
properties of wavelets but also oers a high degree of
directionality and anisotropy. Figure illustrates the NSCT
processing scheme [].
2.2. Image Denoising Method Based on NSCT. e objective
of image denoising is to recover an image from its noisy
version. In general, a denoising problem can be described as
follows. Let
𝑖,𝑗
be the original image of size ×and let
𝑖,𝑗
be
the observation image which has been corrupted by additive
white Gaussian noise
𝑖,𝑗
with zero mean and variance
2
.Let
(,)be the pixel position in the image. en, assume that the
corrupted image satises
𝑖,𝑗
=
𝑖,𝑗
+
𝑖,𝑗
,
=1,2,...,,=1,2,...,,
𝑖,𝑗
∼0,
2
.
()
e goal of denoising is to construct the optimal approxi-
mation of
𝑖,𝑗
using the observation data
𝑖,𝑗
to minimize the
mean square error (MSE) between the optimal approxima-
tion
𝑖,𝑗
and the original signal
𝑖,𝑗
:
MSE =
1
−
2
=
1
𝐼
𝑖=1
𝐽
𝑗=1
𝑖,𝑗
−
𝑖,𝑗
2
,
=×.
()
e basic steps in the threshold denoising algorithm are
as follows:
() Determine the decomposition level, ,ofNSCTand
perform NSCT on the noisy image, ,toobtainthe
high and low-frequency coecients of the decompo-
sition.
()Determinethecorrectthresholdvalueandperform
threshold processing on the high-frequency coe-
cients in the NSCT domain to obtain the new trans-
form coecients, while leaving the low-frequency
coecients unchanged. e threshold processing
includes so and hard threshold processing.
() Perform inverse NSCT on the processed high-
frequency coecients and low-frequency coecients
to obtain the denoised image estimation,
,whichis
the estimation of the original image, .
e key issue in threshold denoising is selection of the
threshold value, which directly determines the denoising
eect. A relatively small threshold value may retain the
decomposition coecients as much as possible and thus
retain more detailed information about the image. However,
a small threshold value may retain an undesired amount of
noise in the denoised result. Conversely, a relatively large
threshold value may destroy the high-frequency information
of the image and produce a false Gibbs phenomenon in the
denoised image.
3. Marginal Statistical Modelling on the NSCT
Subband Coefficients
3.1. Normal Inverse Gaussian Distribution. e important
featuresoftheimagestatisticsintheNSCTdomainisthat
they are non-Gaussian, have a high kurtosis, sharp central
peak, and heavy tails. ese features are expected because
images oen primarily comprise homogeneous regions with
some important details such as edges; the homogeneous
regions provide coecients that are close to zero, and the
edges provide a small number of coecients with large
magnitudes. e NIG model developed by Barndor-Nielsen
[] is a normal variance-mean mixture distribution, in
which the inverse Gaussian PDF is used as the mixing
distribution. In theory, the hybrid model can overcome the
disadvantages of the traditional model, which cannot meet
the needs of modelling. Because of the exibility with which
parameters can be selected, the hybrid model can describe
curves of any shape. Consequently, we chose the NIG model









