Python有限元分析：8-14-20节点立方体弹性固体三维模拟

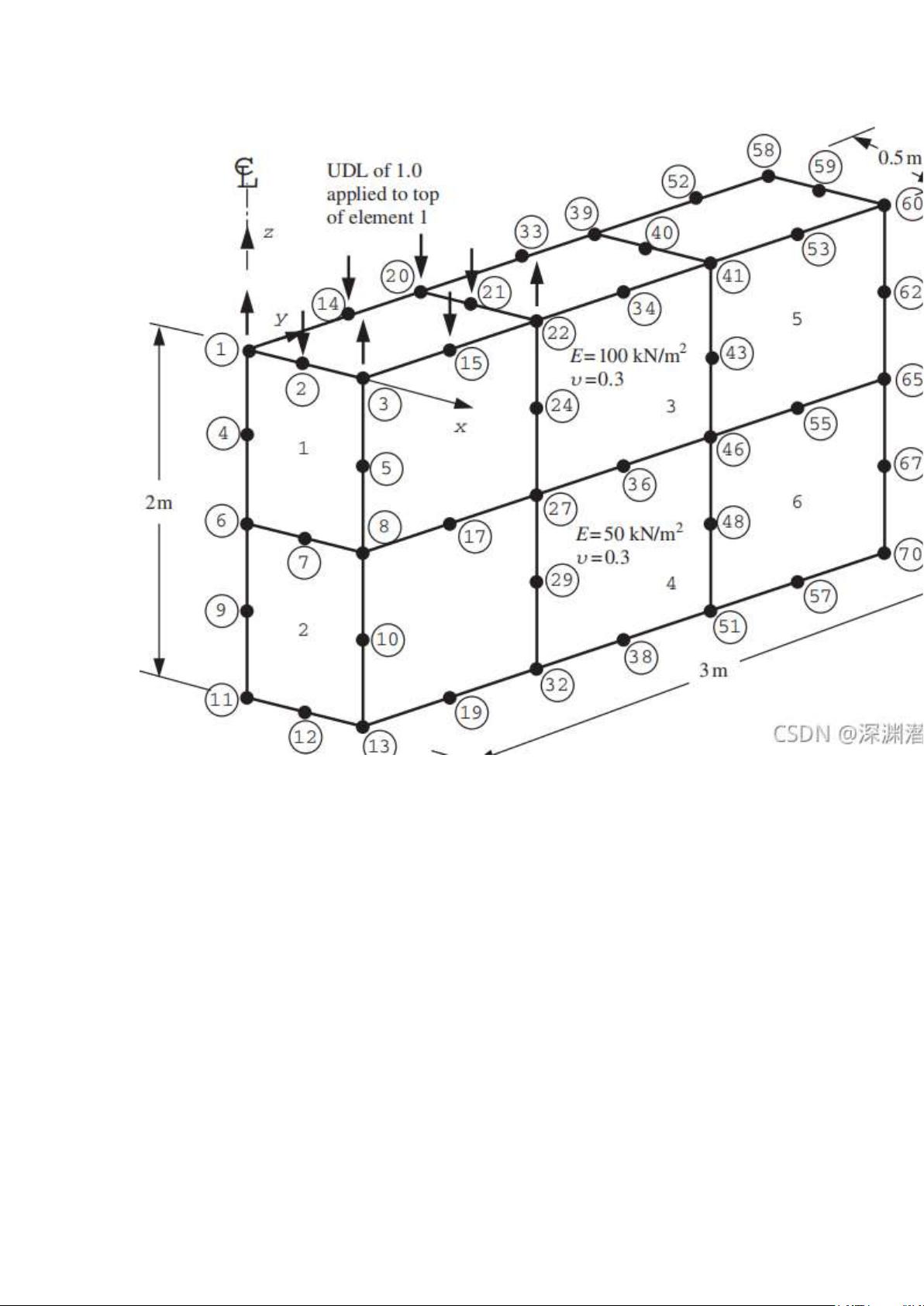
该资源是一个关于使用Python进行三维弹性固体分析的程序，主要涉及8、14、20节点的六面体网格划分。通过有限元方法，对立方体弹性固体进行建模和求解。程序参考了第七篇的内容，并且提供了一个内置几何子程序hexahedron_xz，用于生成yz平面开始并沿y方向扩展的节点和单元标号。计算实例中，设置了不同的节点值、网格划分、积分点数量以及单元性质，包括弹性模量和泊松比。此外，还定义了约束节点和荷载节点，以及相关的荷载值。 详细知识点： 1. **有限元方法(Finite Element Method, FEM)**：此程序基于有限元方法，是一种用于数值解决各种工程和物理问题的通用方法，特别适用于复杂几何形状和非线性问题的求解。 2. **Python编程**：程序使用Python作为编程语言，Python在科学计算领域有着广泛的应用，因其简洁明了的语法和丰富的库支持。 3. **网格划分**：网格划分是有限元分析的关键步骤，程序使用8、14、20节点的六面体网格，不同节点数量对应不同的精度需求。在这个例子中，x方向划分1个单元，y方向划分3个，z方向划分2个。 4. **积分点**：积分点的数量影响着有限元求解的精度，20节点六面体通常需要较多积分点，但为了简化，程序选择了8个积分点。 5. **单元性质**：单元性质包括弹性模量(e)和泊松比(v)，在实例中，存在两种不同的单元属性，即e=100.0、v=0.3和e=50.0、v=0.3，它们被分配给不同的单元。 6. **约束与荷载**：约束节点46个，表示对某些节点的自由度进行限制，例如节点1的x和y方向被约束。荷载节点8个，仅在z方向施加荷载，荷载值为一组特定的数值。 7. **numpy库**：在Python中，numpy库用于处理大型多维数组和矩阵，它是科学计算的基础库，程序中用于创建和操作数组。 8. **自定义函数**：程序中的`hexahedron_xz`是自定义的几何子程序，用于生成六面体的节点和单元编号。 9. **数据结构**：如`nels`、`nn`、`nf`、`points`、`g`等变量，用于存储单元数量、节点数量、节点自由度分配、积分点坐标和全局节点数组等关键信息。 10. **维度和自由度**：在三维空间中，每个节点有3个自由度（x、y、z方向的位移），总自由度等于节点数乘以自由度数。 11. **代码组织**：程序的代码结构包括变量初始化、网格生成、节点和自由度数组定义、荷载和约束的设定等部分。 这个程序展示了如何利用Python和有限元方法进行三维弹性固体的数值分析，对于学习和理解有限元法在实际问题中的应用具有一定的指导价值。