March 10, 2011 / Vol. 9, No. 3 / CHINESE OPTICS LETTERS 032201-1
Optical system design with conformal
decentered and tilted elements
Jun Chang (~~~ )
1∗
, Wubin He (ÛÛÛÎÎÎRRR)
1
, Ruirui Wang (```aaa)
1
, and Shulong Feng (¾¾¾äää999)
2
1
Lab oratory of Optoelectronics Technology and Information System, Scho ol of Optoelectronics,
Beijing Institute of Technology, Beijing 100081, China
2
Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 343100, China
∗
Corresp onding author: bitchang@bit.edu.cn
Received Septemb er 7, 2010; accepted November 15, 2010; posted online February 21, 2011
We investigate the aberration properties of the conformal optical system with decentered and tilted ele-
ments by vector aberration theory. By decentering and tilting the window and corrector of the system,
two elements are effectively used together in a particular manner by aberration compensation to achieve
off-axis imaging. A conceptual design is performed with a half-field of 2
◦
, the F# of 4, and the wave-
length ranging of 3700−4800 nm. The imaging quality can reach the optical diffraction limit and satisfy
corresp onding requirements.
OCIS co des: 220.4830, 220.1010.
doi: 10.3788/COL201109.032201.
At present, increasing number optical devices are begin-
ning to adopt decentered and tilted optical system
[1−5]
.
Some of them are based on the consideration of imag-
ing performance, such as non-obscuration with large field
optical systems; some are based on the consideration of
overall structure, such as in the need to place other non-
optical components on the axis of a system (electronic
components or mechanical components, etc.); others are
applications in special areas, such as projection display
systems of perspective helmets
[6,7]
.
A conformal optical system, with its excellent aero-
dynamic performance, is drawing increasing attention,
and will be widely applied to various types of aircraft
[8]
.
A conformal window can be coaxial or off-axis, such
as the free form of Airfoil, etc. Multiple institutes
have conducted systematic research on coaxial opti-
cal systems, including dynamic performance, aberra-
tion characteristics
[9]
, and optical correction devices
design
[10,11]
. However, few studies focusing on non-
coaxial optical systems have been conducted, and even
domestic literature on this point is limited. First, design-
ing decentered and tilted optical systems is difficult, and
the aberration theory of current designs for coaxial opti-
cal systems cannot be directly applied to decentered and
tilted optical systems. Second, the non-central symmetry
aberration is rather complicated for conformal windows;
thus, the application of off-axis aberration theory in con-
formal optical systems will be a very significant attempt.
In this letter, we review the vector aberration theory
of decentered and tilted optical systems and analyse the
aberration characteristics of conformal systems with the
decentered windows. According to the aberration char-
acteristics of the conformal system, the spherical aberra-
tion, coma, and astigmatism terms in wavefront polyno-
mials are selected. Then, we adopt aberration compen-
sation methods, and make appropriate decentered and
tilted adjustments on the optical corrector to eliminate
the image effect from the decentered window. Finally,
we analyze the spot diagrams and modulation transfer
function (MTF) curves through optical design software.
Results show that this method can address the challenges
in off-axis conformal optical systems.
In a centered, rotational symmetric optical system, the
Seidel polynomial of wavefront aberration in vector form
is
[12]
:
W =
∑
j
W
j
=
∑
j
W
040j
(~ρ · ~ρ)
2
+
∑
j
W
131j
(
~
H · ~ρ)(~ρ · ~ρ)
+
∑
j
W
222j
(
~
H · ~ρ)
2
+
∑
j
W
220j
(
~
H ·
~
H)(~ρ · ~ρ)
+
∑
j
W
311j
(
~
H ·
~
H)(
~
H · ~ρ), (1)
where
~
H is the normalized field point height; ~ρ de-
notes the normalized pupil redius coordinates; W
j
rep-
resents the optical path difference of actual wavefront
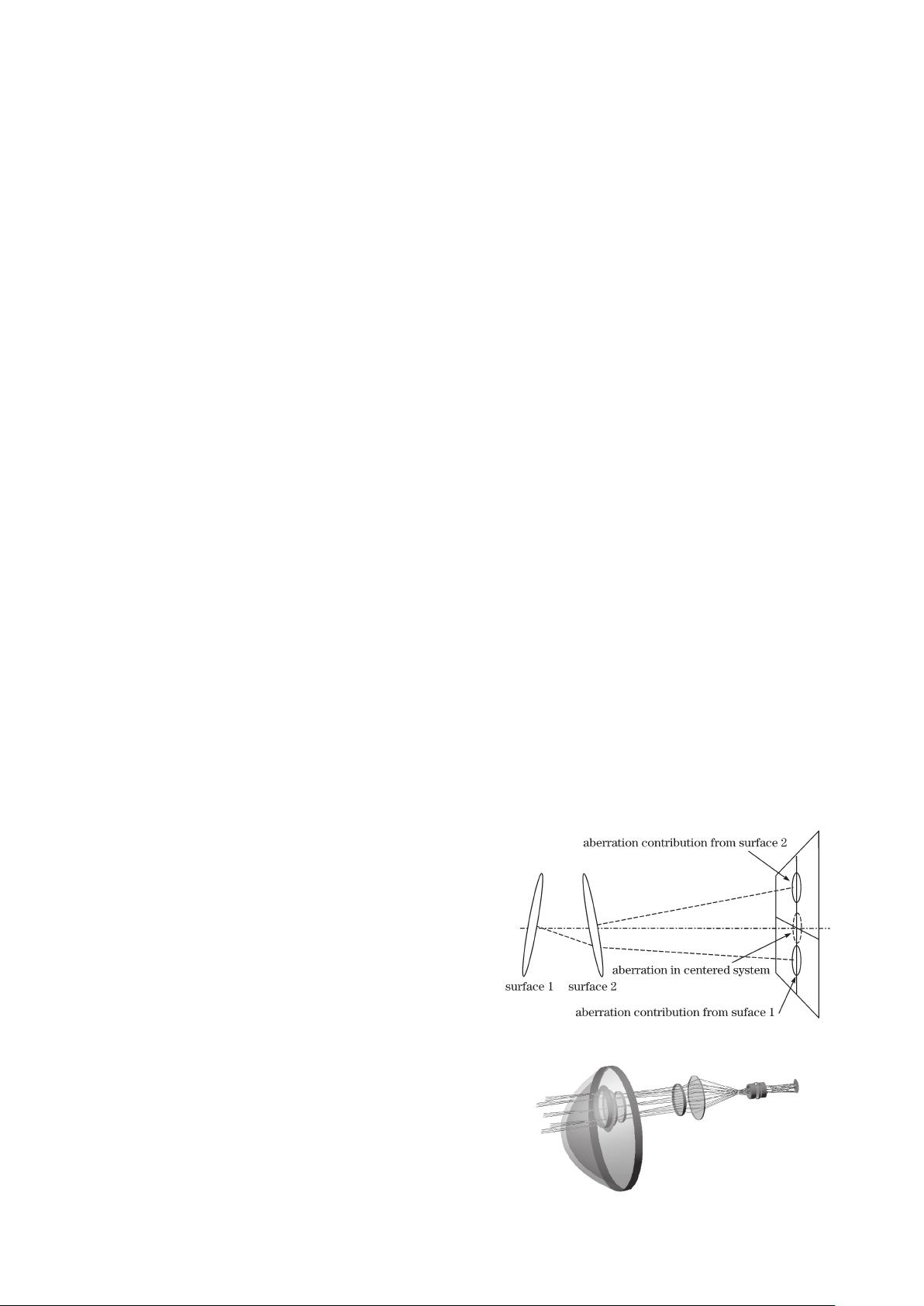
Fig. 1. Decentered and titled aberration contributions from
rotationally symmetric subsystems.
Fig. 2. Decentered window 20 mm.
1671-7694/2011/032201(4)
c
° 2011 Chinese Optics Letters









