Matlab实现贝叶斯与Fisher线性及BP神经网络的机器学习示例

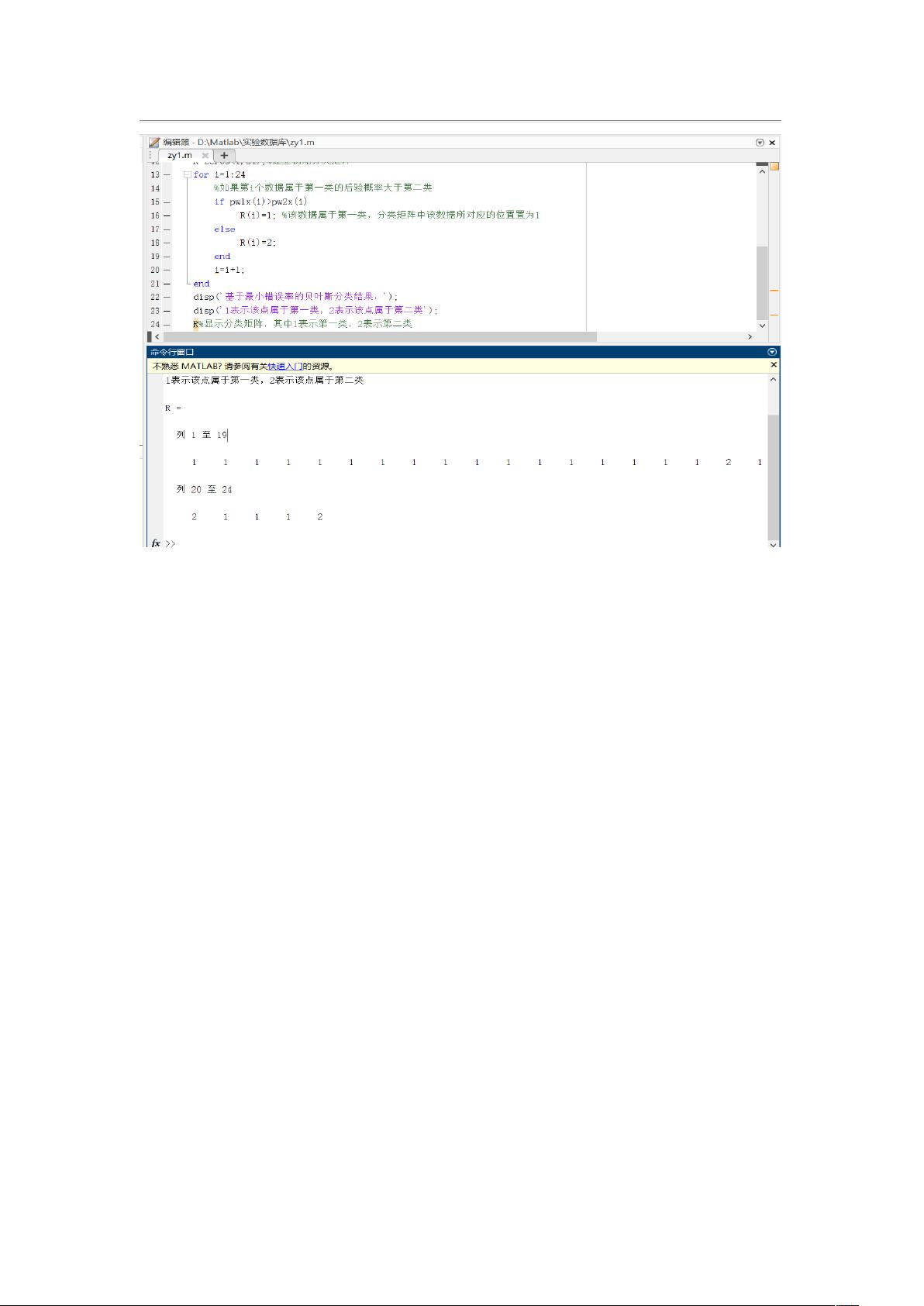
本篇文档主要介绍了在MATLAB中实现贝叶斯分类器的方法，结合特定的生物医学案例进行详细解释。首先，我们了解到这是一个关于局部区域细胞识别的问题，其中正常（P(w1) = 0.9）和非正常（P(w2) = 0.1）两种状态的概率分布遵循正态分布。给定的数据集包含一系列待观察的细胞观测值，以及两类类条件概率：P(x|w1) 对应于正态分布 (-2, 1.5)，P(x|w2) 对应于正态分布 (2, 2)。 贝叶斯决策理论在此处的应用是基于最小错误率原则，即选择最有可能减少错误分类的决策。风险决策表给出了不同错误类型的成本：λ12 = 7（正常误判成本）、λ21 = 2（非正常误判成本），而λ11 和 λ22 为零，表示误判成本相同，这里假设它们不重要。 代码中，首先通过`normpdf`函数计算每个数据点在每类的类条件概率，然后根据先验概率和类条件概率计算后验概率。后验概率反映了在给定观测值下，数据属于某一类别的可能性。接着，通过遍历数据并比较后验概率，将每个数据点分配到分类矩阵`R`中，1代表第一类，2代表第二类。 最后，代码展示了分类结果，即每个数据点被归类为正常或异常状态。通过这个例子，我们可以了解如何在MATLAB中利用贝叶斯分类器处理实际问题，并通过最小化错误率来做出决策。 此外，文章可能还会涉及其他两个MATLAB实现的机器学习模型，如Fisher线性分类器和BP神经网络，但具体的内容未在提供的部分中给出。这些内容可能包括Fisher线性判别法的原理与MATLAB实现步骤，以及如何训练和测试BP神经网络模型，以解决更复杂的问题。对于深度学习部分，如果涉及到MATLAB，可能会讨论使用Neural Network Toolbox或其他相关的工具库来构建和优化深度神经网络结构。然而，由于这部分内容没有提供，因此这里重点分析了贝叶斯分类器的实现。