MATLAB离散傅里叶变换及应用:序列信号的DFT和IDFT求解与比较
90 浏览量
更新于2024-01-21
1
收藏 94KB DOC 举报
MATLAB 离散傅里叶变换及其应用
本文将介绍MATLAB离散傅里叶变换(DFT)及其应用。DFT是一种在实际中经常使用的变换方法,它可以对有限长序列进行频域分析。DFT和逆变换(IDFT)可以用于计算一个信号的频谱及其时域表示。本文将以一个具体的例子来说明DFT和IDFT的应用。
首先,我们有一个有限长序列信号x(n),其取值为[0,1,2,3,4,5,6,7]。我们需要计算该序列的DFT和IDFT。
根据公式(12-1),可以得到该序列的DFT:
X(k) = 1/N * Σ [x(n) * W^(-nk)] (n = 0 to N-1)
根据公式(12-2),可以得到该序列的IDFT:
x(n) = 1/N * Σ [X(k) * W^(nk)] (k = 0 to N-1)
其中,W是单位复数,满足W = exp(-j*2*pi/N)。N为序列的长度。
我们可以根据上述公式,使用MATLAB来计算出序列x(n)的DFT和IDFT。以下是MATLAB程序的源代码:
xn = [0,1,2,3,4,5,6,7];
N = length(xn);
n = 0:(N-1);
k = 0:(N-1);
Xk = xn * exp(-j*2*pi/N).^(n'*k);
x = (Xk * exp(j*2*pi/N).^(n'*k))/N;
首先,我们计算出序列x(n)的DFT,即X(k)。然后,我们利用IDFT公式计算X(k)的逆变换,即得到序列x(n)。
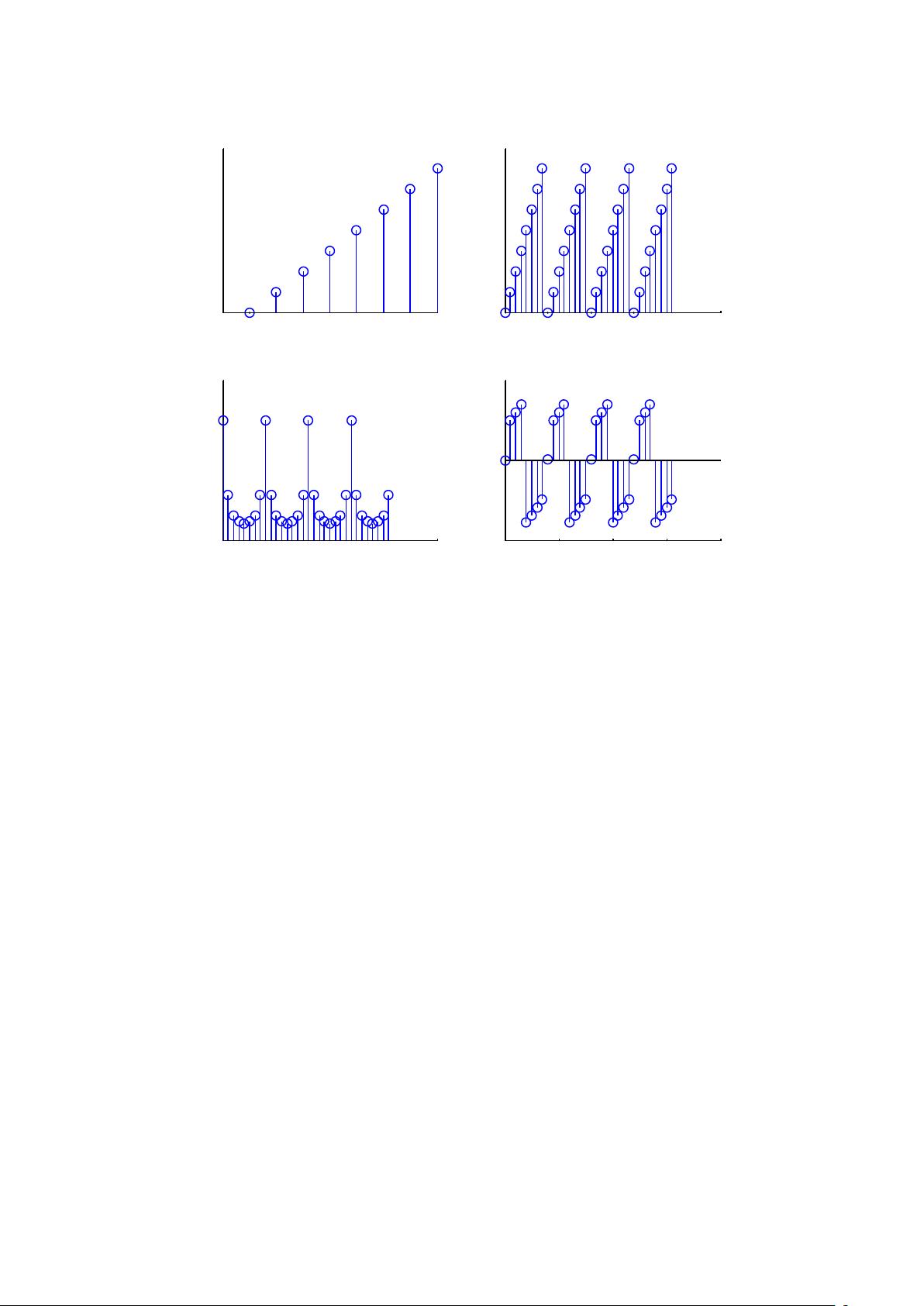
接下来,我们可以使用MATLAB绘制出序列傅里叶变换的幅度谱|X(k)|和相位谱arg[X(k)]。我们可以使用MATLAB的subplot函数将这两个图形放在同一个图窗中。
subplot(2,2,1);
stem(n, xn); % 绘制原始序列
title('原始序列');
xlabel('n');
ylabel('x(n)');
subplot(2,2,2);
stem(k, abs(Xk)); % 绘制幅度谱
title('幅度谱 |X(k)|');
xlabel('k');
ylabel('|X(k)|');
subplot(2,2,3);
stem(k, angle(Xk)); % 绘制相位谱
title('相位谱 arg[X(k)]');
xlabel('k');
ylabel('arg[X(k)]');
然后,我们可以将计算得到的x(n)与原信号进行比较,绘制出两者的图形。
subplot(2,2,4);
stem(n, x); % 绘制IDFT的结果
title('IDFT [X(k)]');
xlabel('n');
ylabel('x(n)');
从以上程序运行结果可以看出,序列的傅里叶变换可以将原始序列在频域上进行分析。幅度谱反映了序列的频域特性,相位谱则反映了序列在频域上的相位分布。
通过与原始序列进行比较,我们可以验证DFT和IDFT是否正确。如果结果与原始序列相同,那么说明计算是正确的。
综上所述,本文介绍了MATLAB离散傅里叶变换(DFT)及其应用。通过计算序列的DFT和IDFT,可以得到序列在频域和时域上的表示,并可以进行相应的分析和处理。MATLAB提供了方便的函数和工具,可以帮助我们进行这些计算和分析。对于信号处理和频谱分析等领域的研究者和工程师来说,掌握DFT和IDFT的原理和应用是非常重要的。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2021-10-07 上传
347 浏览量
270 浏览量
138 浏览量
2021-10-09 上传
119 浏览量
xinkai1688
- 粉丝: 390
- 资源: 8万+
最新资源
- 关于sql优化.doc
- 服装行业电子商务平台建设构想.pdf
- JAVA解惑之详细介绍
- sql server 2000
- Java项目开发常见问题分析
- accp5.0s2三层+OOP测试
- css常用参数说明文档
- Websphere Appliction Server Development Best Practices for Performance and Scalability.pdf
- 高质量C++编程指南.pdf
- FastReport_3.0_设计手册PDF
- The_C_Programming_Language_2nd_edition
- Test Automation Frame--主要框架的介绍.doc
- tuxedo编程速成
- JBossWeb用户手册
- PHP5与MySQL5 Web开发技术详解.pdf
- 很好的linux学习笔记