MATLAB中FFT算法实现与离散系统分析

本次实验报告针对信工3班201630258438蒲尧同学的课程，主要关注离散系统的频率响应分析和FFT（快速傅立叶变换）算法在MATLAB中的应用。实验的主要目标包括： 1. **深化离散信号DFT的理解**：实验通过实际操作，使学生更深入地掌握离散傅立叶变换(DFT)的基本概念和其在离散信号处理中的作用，理解离散信号在频域的表示。 2. **MATLAB中的FFT算法实现**：实验要求学生预习并熟练掌握MATLAB中的fft和ifft函数，通过实例学习如何在该软件中实现FFT算法，这不仅锻炼了编程技能，也提升了数字信号处理的实际应用能力。 3. **频率响应分析方法**：实验强调了对离散系统频率响应分析的理解，这是通信系统设计和信号处理中不可或缺的一部分，有助于学生理解和评估系统的性能。 4. **零、极点分布的理解**：通过实验，学生将进一步理解零点和极点在信号系统的动态特性中的重要性，这对系统的稳定性分析至关重要。 **实验步骤与预习要求**： - 学生需预先熟悉MATLAB中的fft和ifft函数的使用，确保能够在代码中正确调用它们进行DFT计算。 - 阅读扩展练习中的实例，通过具体案例学习FFT算法的实现流程，包括如何输入数据、调用函数、解读结果等。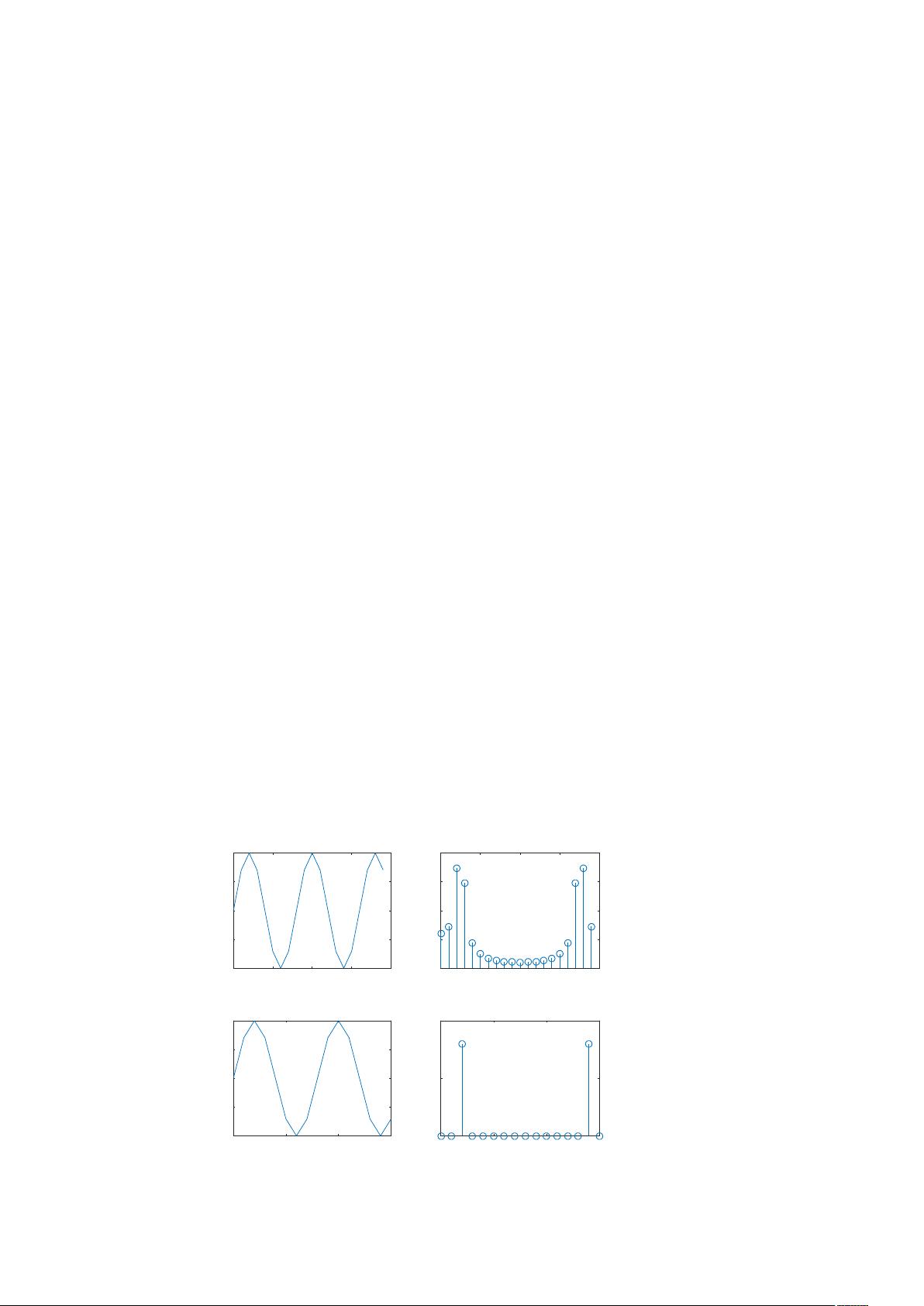 - 实际操作中，学生需要编写MATLAB脚本，对一个连续的单一频率周期信号进行采样（如fs=8fa），然后选择不同的采样长度N（如N=20和N=16），计算其DFT并绘制幅度谱，对比理论计算，分析实验结果的差异及其原因。 **安全与纪律要求**： 实验过程中，学生必须严格遵守电子与信息学院的学生实验守则，确保个人安全和实验室设备的完好。这包括但不限于预习、准时参加、遵守操作规程、爱护仪器、保护数据安全、及时报告事故以及撰写真实完整的实验报告。 通过这次实验，学生不仅能够提升数学模型与实际应用的结合能力，还能培养严谨的科学态度和良好的实验习惯，为后续的科研和工程实践打下坚实的基础。