MATLAB实现系统聚类分析：从理论到实践

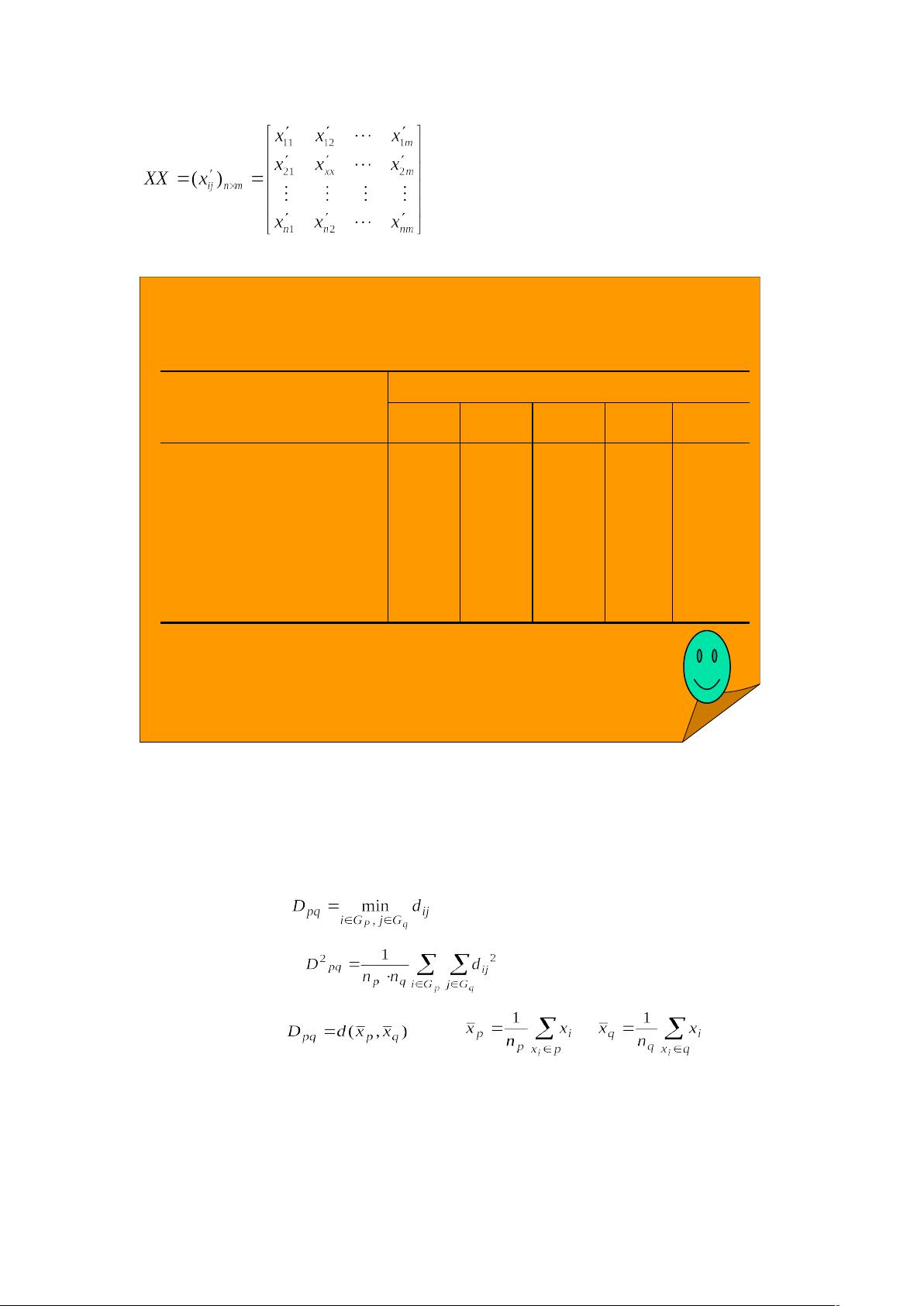
"这篇文档介绍了系统聚类算法的MATLAB实现，主要关注系统聚类法的基本概念、距离计算方法以及MATLAB中的实现步骤。系统聚类法是一种无监督的分类方法，适用于各种领域的数据分析，如考古学、地质学、气象学等。文中详细阐述了如何基于样品间的距离进行聚类，并探讨了闵可夫斯基距离的不同形式，包括绝对值距离、欧氏距离和切比雪夫距离。此外，还提到了在处理不同量级和单位的指标时的预处理需求。" 系统聚类法是一种多元统计分析技术，用于对没有预设分类的数据集进行分组。它基于样品之间的相似性或距离进行操作，目的是找到内在的结构或者自然的群组。在实际应用中，系统聚类通常用于那些没有先验知识或模式的情况，通过对大量样品的特征进行分析来构建分类。 在系统聚类中，样品之间的距离是关键的度量标准。闵可夫斯基距离提供了一种通用的计算方式，公式为 [pic]，其中[pic] 是特征变量的个数，[pic] 和 [pic] 分别代表两个样品，[pic] 是权重参数。当[pic] 为1时，该距离变为曼哈顿距离（绝对值距离）；当[pic] 为2时，得到的是欧氏距离；而[pic] 为无穷大时，得到的是切比雪夫距离。这些距离定义考虑了不同特征变量的重要性，特别是在数据尺度不一时。 在MATLAB中实现系统聚类，通常会调用特定的函数，例如`linkage`函数，它可以计算样品之间的相似性矩阵，并生成树状图（dendrogram）。此外，`cluster`函数可以用来切割链接树，从而确定最终的聚类。在使用这些函数前，可能需要对数据进行标准化处理，确保各特征在同一尺度上，以避免某些特征因为较大的数值范围而占据主导地位。 在实际操作中，需要注意的是，距离计算可能会受到观测值数量级和单位的影响。例如，不同特征的数值范围相差悬殊时，直接计算可能会导致某些特征的影响被忽略。因此，在进行聚类分析之前，通常需要对数据进行预处理，如标准化或归一化，确保所有特征对聚类的影响平等。 上机作业部分可能涉及到应用这些理论知识，实际编写MATLAB代码，执行系统聚类并分析结果。这可能包括读取数据、计算距离矩阵、选择合适的链接方法（如单链接、全链接或平均链接）、生成聚类树并进行解释。通过这样的实践，可以加深对系统聚类算法的理解，并掌握其在实际问题中的应用。