贪心算法详解与应用示例

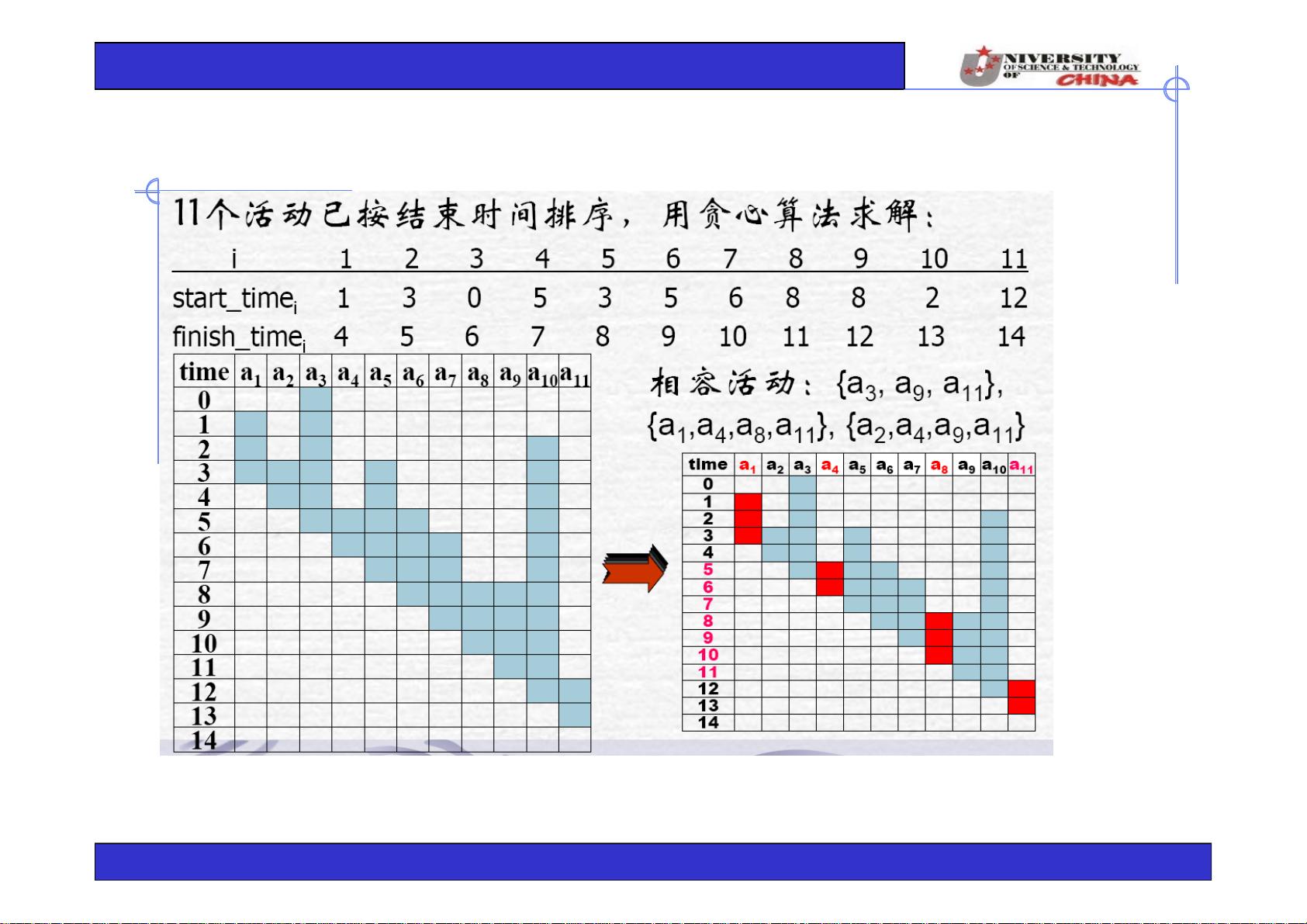
"本资源主要介绍了贪心算法的概念、基本要素和设计策略，以及通过活动安排问题来阐述贪心算法的应用。贪心算法是一种在每一步选择中都采取在当前状态下最好或最优的选择，从而希望导致结果是全局最好或最优的算法。与动态规划不同，贪心算法不一定能得到整体最优解，但在某些问题上，如单源最短路径和最小生成树问题，它能产生整体最优解或接近最优解的结果。" 贪心算法是计算机科学中的一种解决问题的方法，它通过每次选取局部最优解的方式来尝试达到全局最优解。在贪心算法中，我们并不考虑整个问题的全局最优解，而是每一步都做出看似最佳的选择。这种策略在一些问题上非常有效，尤其是在问题具有最优子结构的情况下，即局部最优解能组合成全局最优解。 在描述中提到的活动安排问题是一个经典的贪心算法应用实例。问题背景是有一系列活动需要在同一资源上进行，但同一时间只能进行一个活动。每个活动都有开始时间和结束时间，两个活动如果在时间上不重叠，那么它们就是相容的，可以同时进行。目标是找到最大数量的相容活动子集。贪心算法在这种问题上的策略通常是按结束时间从小到大排序活动，然后依次选择第一个未被排除的活动，因为这样能确保每个被选中的活动都是在当前未被占用时间段内的最优选择。 动态规划通常用于解决具有最优子结构的问题，它会通过构建子问题并存储子问题的解来避免重复计算，最终得到全局最优解。与贪心算法不同，动态规划会考虑所有可能的子问题组合，而贪心算法则是步步为营，不回溯。 虽然贪心算法在一些问题上无法保证得到全局最优解，但它的效率往往比动态规划更高，因为贪心算法通常不需要回溯和存储大量的中间状态。例如，在单源最短路径问题（如Dijkstra算法）和最小生成树问题（如Prim算法或Kruskal算法）中，贪心算法能够有效地找到最优解。 贪心算法是一种实用的算法策略，尤其在处理局部最优解可导向全局最优解的问题时，它可以提供高效且接近最优的解决方案。然而，对于那些需要全局考虑所有可能性的问题，贪心算法可能就需要结合其他方法，如动态规划，才能找到真正最优的解。