Black-Scholes期权定价理论在金融经济学中的应用

"第八讲BlackScholes期权定价理论(货币金融学).pptx" Black-Scholes期权定价理论是金融工程领域中的一个核心概念，由 Fischer Black 和 Myron Scholes 在1973年提出，用于计算欧式期权的公平价格。这个理论是基于无摩擦市场假设，包括无交易成本、无税收、无限制的借贷、即时执行的交易以及完全的信息等。它主要解决了如何在股票价格随机波动的情况下，确定期权价格的问题。 8.1 Black-Scholes 欧式买入期权定价公式 Black-Scholes公式是计算欧式看涨期权价格的数学表达式，其中包括五个关键变量： 1. S：股票当前价格 2. K：期权的执行价格（行权价） 3. T：期权到期时间（以年为单位） 4. r：无风险利率 5. σ：股票价格的对数收益率的标准差（即波动率） 公式可以表示为 C = SN(d1) - Ke^(-rT)N(d2)，其中C是期权价格，N()是标准正态分布的累积分布函数，d1和d2是与这些变量相关的复合分数。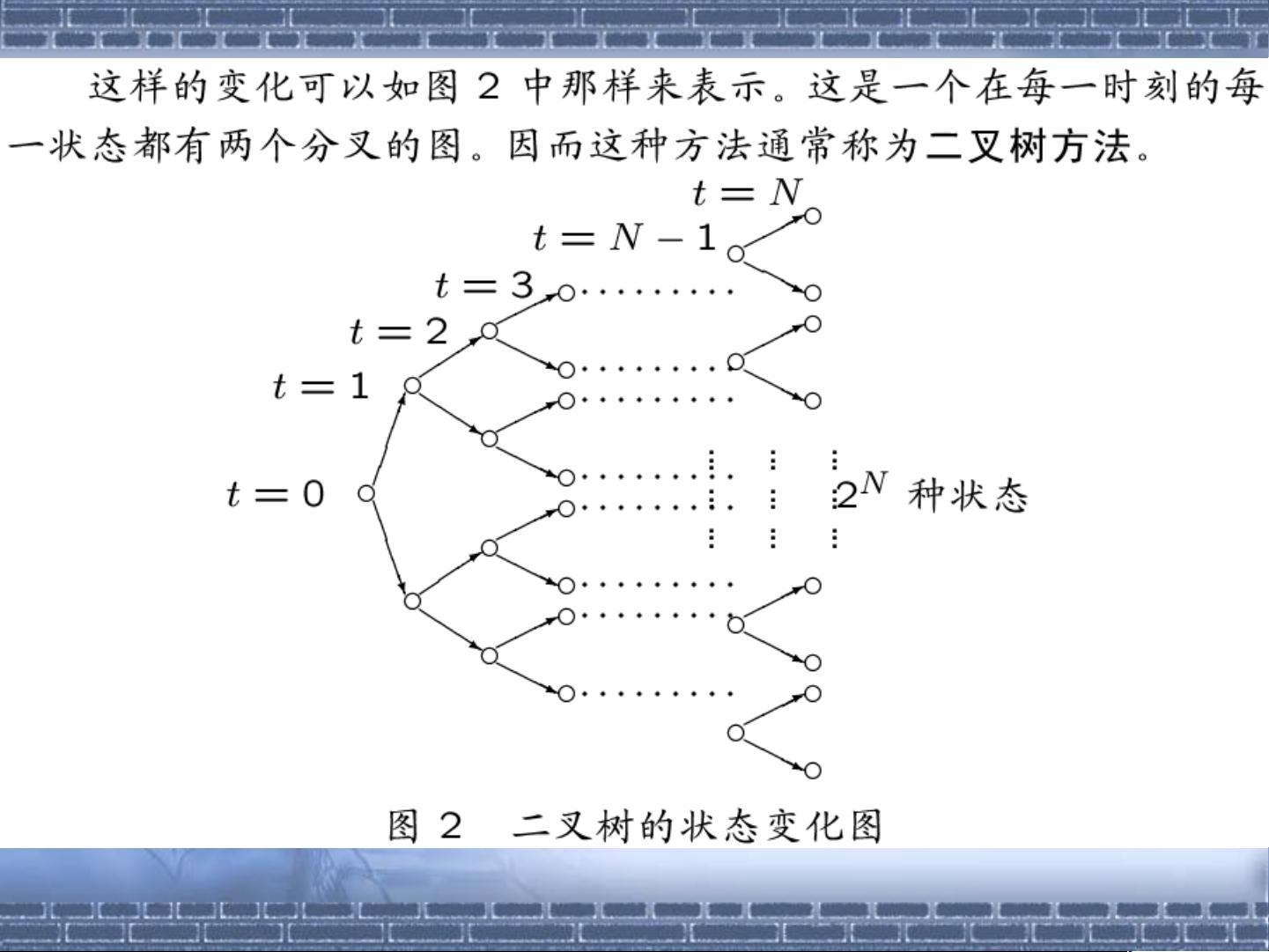 8.2 Black-Scholes公式的前驱 Black-Scholes模型的形成并非一蹴而就，它的建立受到了许多先驱工作的影响，包括： - John Cox、Ross 和 Rubinstein 提出的二叉树方法（Cox-Ross-Rubinstein model），为Black-Scholes模型提供了一个直观的离散化框架，通过将连续时间过程分解为一系列的二元选择，逐步逼近期权价格。 - Ito's Lemma（伊藤引理）在随机微积分中的应用，它帮助建立了Black-Scholes方程的基础数学框架。 - Martingale理论和Brownian motion（布朗运动）理论，这些都是现代金融数学的基石，它们描述了股票价格的随机运动。 8.3 Black-Scholes公式的Cox-Ross-Rubinstein(二叉树方法)推导 Cox-Ross-Rubinstein模型使用二叉树模型来模拟股票价格在到期日之前的可能路径。在这个模型中，股票价格在每个时间步只能向上或向下跳跃一个固定比例。通过迭代计算每个时间步所有可能的股票价格和对应的期权价值，最终可以求得期权的公平价格。 Black-Scholes模型的其他内容包括： - 对于卖出期权（Put Option），有相应的Black-Scholes公式，可以通过买入期权公式进行调整。 - 看跌-看涨平价关系（Put-Call Parity）揭示了看涨期权和看跌期权之间的基本联系，即使在没有Black-Scholes公式的情况下，也可以利用这一关系定价。 - 波动率是Black-Scholes模型中的关键参数，对期权价格有很大影响。实际市场中，波动率是动态变化的，因此Black-Scholes模型常用于估算隐含波动率。 J.J. Laffont关于一般经济均衡与期权定价理论的讨论指出，即使在没有特定的期权市场时，资产的反复交易也能产生Arrow-Debreu均衡，这表明期权定价不仅限于有形的期权市场，而是整个金融市场均衡的一部分。 Black-Scholes期权定价理论是现代金融学的里程碑，它提供了理解和计算期权价格的理论基础，并影响了金融市场的实践操作。然而，理论的应用需要考虑现实世界的复杂性，如交易成本、市场摩擦和不对称信息等因素。