MATLAB编程实现一维热传导方程数值解比较与自由振动问题周期解求解

本资源是一份关于偏微分方程数值解的上机报告，主要涉及MATLAB编程在求解热传导方程和自由振动问题中的应用。实验内容分为两部分： **实验内容1：一维热传导方程求解** 该部分使用了三种不同的差分格式——向前差分格式、向后差分格式以及六点对称格式来求解一维热传导方程。方程为 \( \frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2} \)，边界条件和初始条件已给出。具体步骤包括： 1. **算法描述**： - 向前差分格式通过逐次逼近时间步进，每一步使用当前时刻的值来估计下一时刻的值。 - 向后差分格式则是利用未来时刻的信息来估计当前时刻，适用于稳定性较差但精度较高的情况。 - 六点对称格式结合了前后两种方法的优点，提供更高的精度。 2. **实验结果**： - 对于三种格式，提供了MATLAB代码示例（forward、back、six函数）和相应的误差数值解结果。 - 在0.25单位时间后，可以看出六点对称格式的误差最小，数值解与精确解的差异较小。 3. **结果分析**： 结果表明这三种方法都可用于解决该热传导问题，但六点对称格式在精度上表现出色。 **实验内容2：自由振动问题求解** 实验的第二部分是使用差分法求解自由振动问题，方程形式为 \( \frac{\partial^2 u}{\partial t^2} = -k^2 u \)（忽略重力加速度），涉及周期解的计算。网格剖分和离散化过程在报告中也有所提及。 4. **算法描述**： - 包括网格划分、时间步进以及使用特定的差分方法求解波动方程。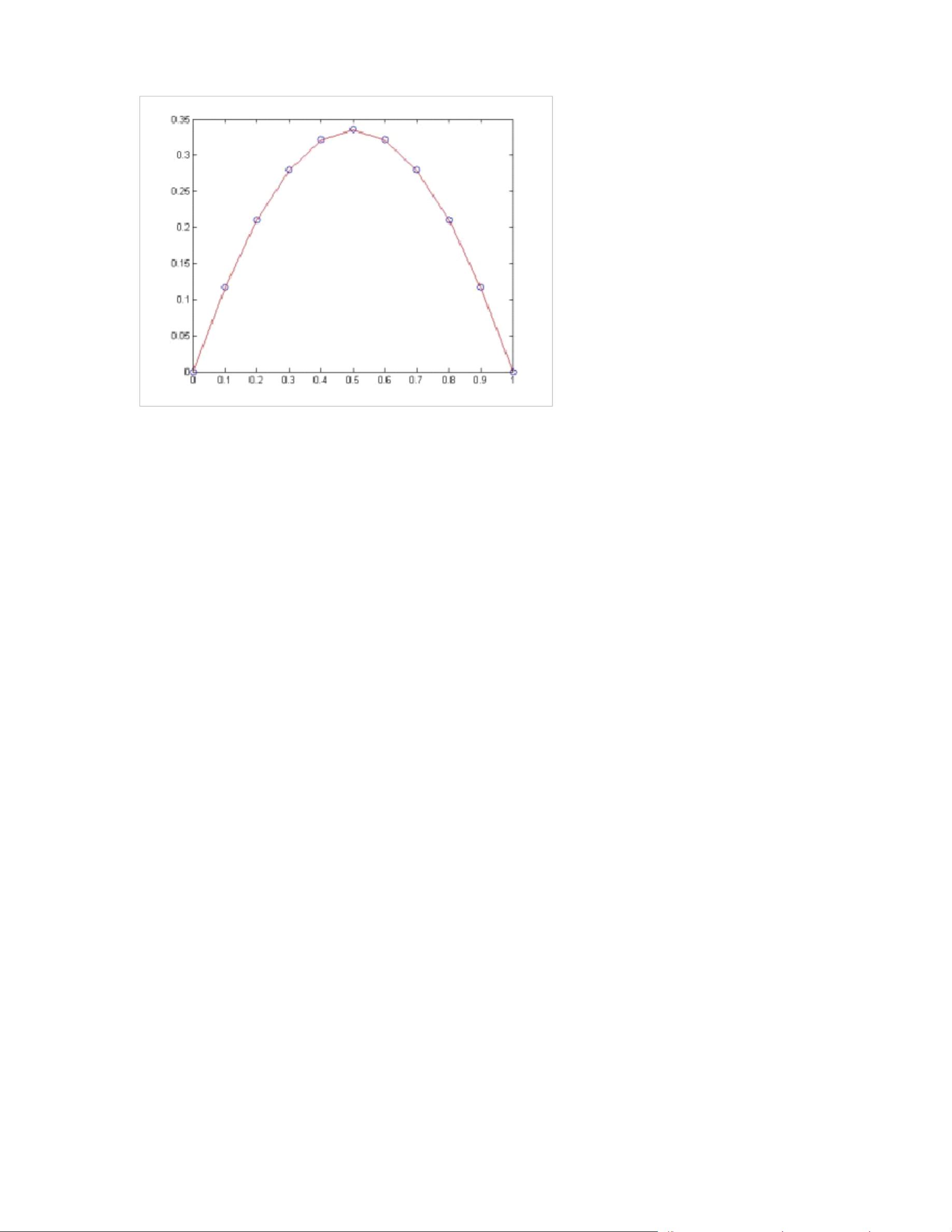 5. **图像对比**： - 提供了精确解与数值解的图形比较，以直观展示求解效果。 总体而言，这份报告展示了在MATLAB环境下使用差分方法求解偏微分方程的实际操作，并强调了六点对称格式在提高求解精度方面的优势。通过这些实例，学习者可以深入理解不同差分格式的适用场景和性能优劣，为实际工程问题的数值求解打下基础。