海赛矩阵：计算、特性与优化问题应用

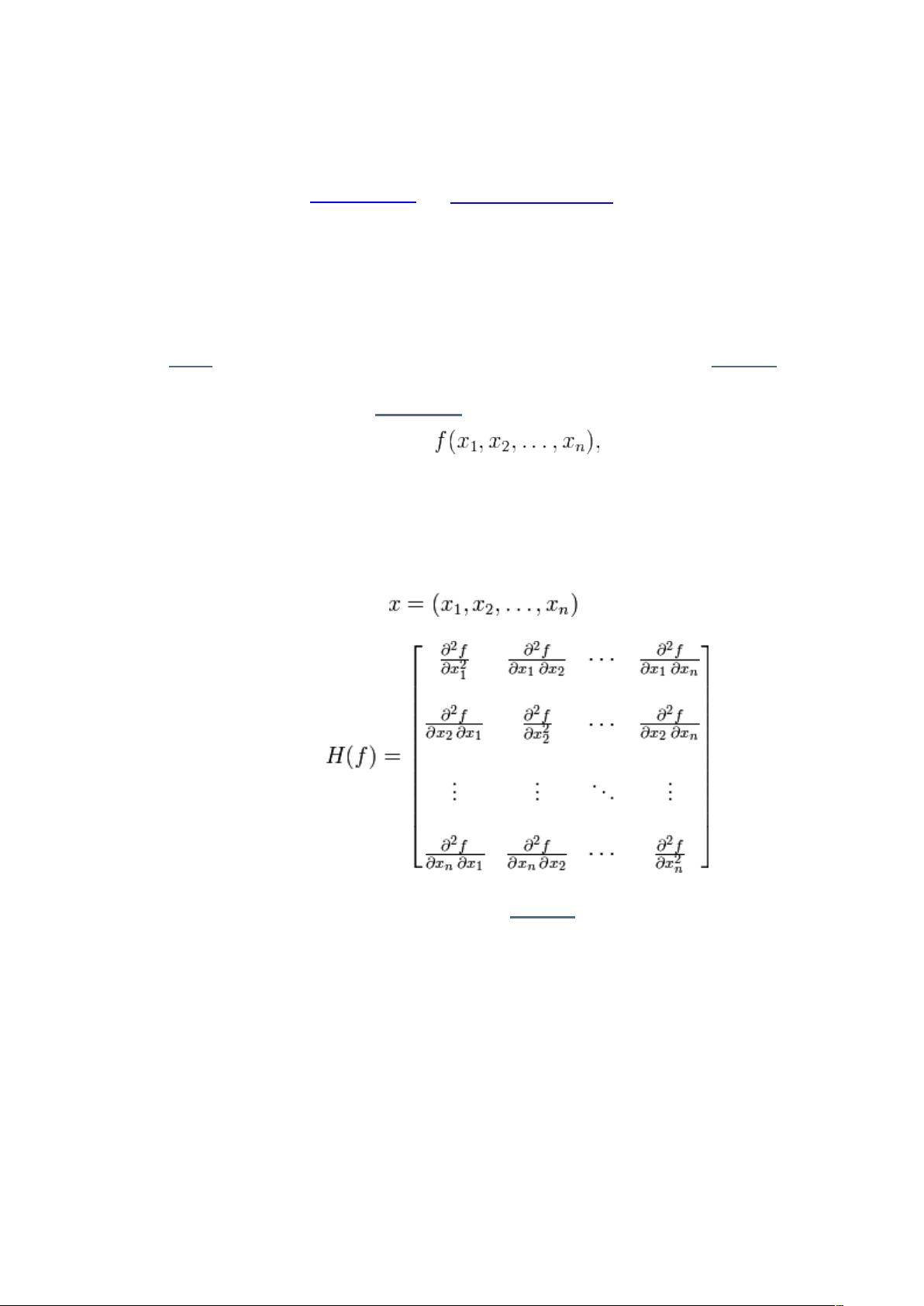
"海赛矩阵，也称为Hessian矩阵，是多元函数二阶偏导数构成的方阵，用于描述函数的曲率信息和在优化问题中的极值判定。" 海赛矩阵是微分几何和多变量微积分中的一个重要概念，由德国数学家卡尔·弗里德里希·高斯的弟子奥古斯特·海色提出。它是一个函数的二阶导数集合，反映了函数在某一点的曲率和形状。对于一个实值函数f: R^n → R，其海赛矩阵H(f)是一个n×n的矩阵，其元素H(f)ij定义为： \[ H(f)_{ij}(x) = \frac{\partial^2 f}{\partial x_i \partial x_j}(x) \] 这里，\( \frac{\partial}{\partial x_i} \) 表示对第i个变量的偏导数，而 \( x \) 是函数f的n维输入向量。如果函数f的所有二阶偏导数都在某区域D内存在且连续，那么海赛矩阵在D内是对称的，因为混合偏导数相等： \[ \frac{\partial^2 f}{\partial x_i \partial x_j}(x) = \frac{\partial^2 f}{\partial x_j \partial x_i}(x) \] 海赛矩阵在实际应用中，特别是在优化问题中，起到关键作用。例如，在牛顿法中，海赛矩阵用于近似函数的二次模型，帮助寻找函数的局部极值点。当函数在某点的梯度（一阶导数）为零时，这个点可能是极值点。海赛矩阵的符号可以用来判断这个点是局部极小值、局部极大值还是鞍点。 对于一个二元函数f: R^2 → R，海赛矩阵的行列式，即海色行列式，可以用来判断临界点的性质。如果在临界点(x0, y0)处有： - H > 0: 函数f在(x0, y0)处有一个局部极小值。 - H < 0: 函数f在(x0, y0)处有一个局部极大值。 - H = 0: 这个临界点可能是鞍点，或者需要更高阶的导数来确定其性质。 在多变量函数的最优化问题中，正定的海赛矩阵指示函数在其相应的点具有局部极小值，而负定的海赛矩阵则指示局部极大值。当海赛矩阵的特征值全为正或全为负时，可以根据它们的符号来判断极值类型。如果特征值中有正有负，那么该点是鞍点。 需要注意的是，海赛矩阵的零特征值并不意味着函数在该点没有极值，而是表示需要考虑更高阶的导数，如三阶导数，或者通过其他方法如泰勒展开来确定极值的存在性。在实际应用中，海赛矩阵的计算和分析是数值优化算法和复杂函数分析的基础工具。