图论与数据结构深度解析：算法与数据结构精华总结

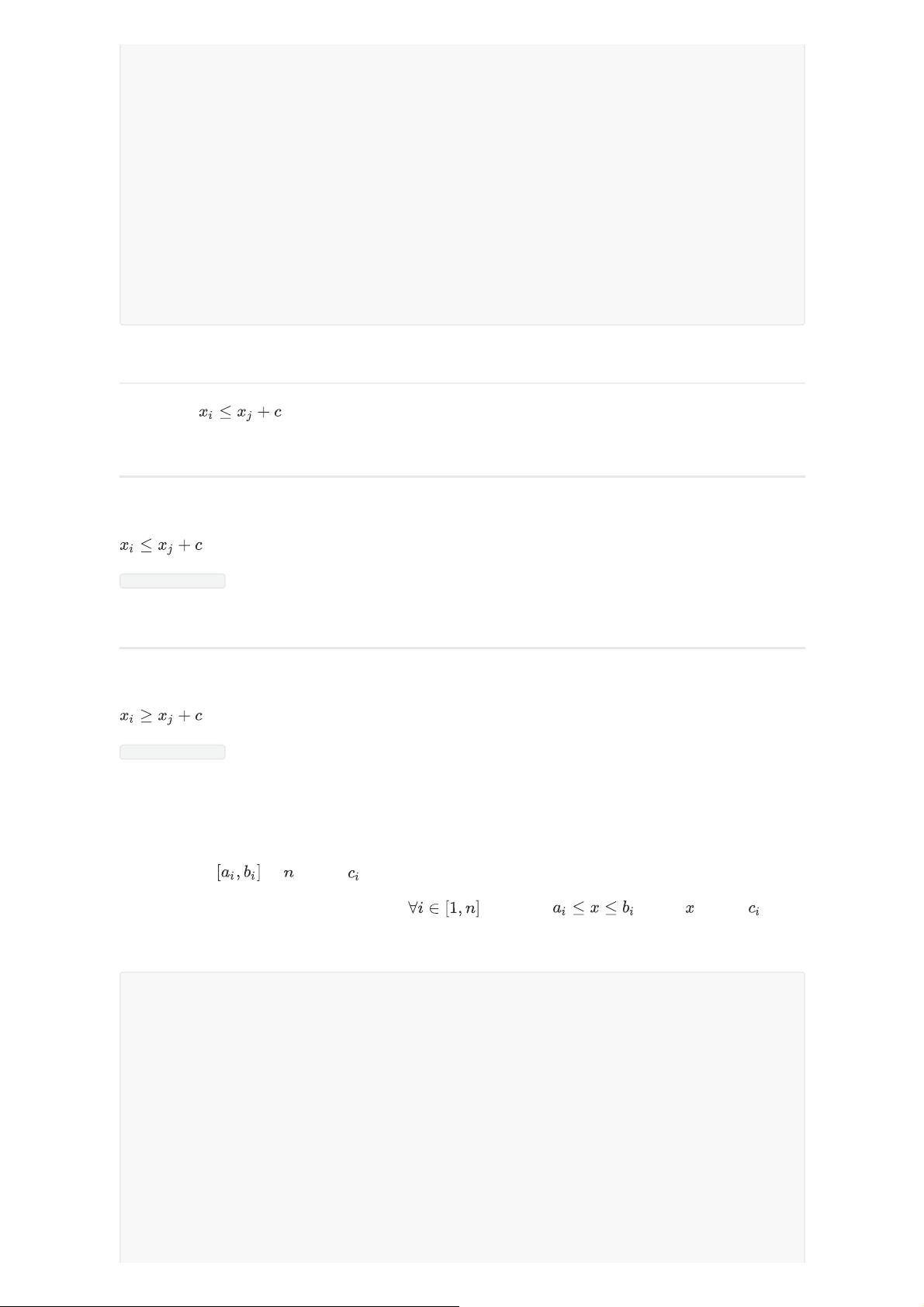
本资源涵盖了广泛的IT领域知识，特别是图论、网络算法和数据结构，以及部分字符串处理和数学原理。以下是对各部分内容的详细解读： 1. 图论：这部分深入探讨了多种经典算法。Dijkstra算法用于寻找两点之间的最短路径，SPFA是其扩展，可用于判断负环；Floyd-Warshall算法用于计算所有节点对之间的最短路径；最小生成树（Prim或Kruskal）讨论了边在生成树中的角色以及严格次小生成树的概念；拓扑排序用于确定节点的执行顺序；差分约束涉及区间操作；倍增求LCA解决了最近公共祖先问题；有向图的强联通分量和无向图的双联通分量是网络连通性的不同划分；染色法和匈牙利算法用于二分图的分析；网络流理论涉及Dinic算法求解最大流、二分图匹配等；2-SAT问题与朱刘算法则是组合优化的一部分。 2. 数据结构：重点介绍了树状数组、线段树及其各种操作，如区间更新和查询；树链剖分用于处理复杂的数据结构；平衡树（如AVL或红黑树）提供了高效查找和插入；此外，还有可持久化数据结构、ST表、分块等高级数据结构。 3. 字符串处理：KMP算法用于字符串匹配，Trie和AC自动机用于高效的模式搜索；计数DP用于统计单词出现频率；哈希技术在字符串处理中有广泛应用；循环同构串的最小表示法和马拉车算法则针对特定字符串问题；后缀数组是字符串分析的重要工具。 4. 数学基础：包括筛素数的几种常见方法（如线性筛、埃氏筛和分段筛）、约数和欧拉函数的计算，以及欧几里得算法和求解特定问题的数学技巧。 这些知识点紧密围绕着计算机科学的核心领域，不仅有助于理解基础数据结构和算法，还涉及了实际问题的解决策略。掌握这些内容对于IT专业人士来说是至关重要的，无论是进行编程实现、设计算法还是优化性能，都能提供坚实的基础。