MATLAB中的数字信号处理实验：时域离散系统响应

"该资源是一系列关于MATLAB中数字信号处理的实验，涵盖了从实验1到实验4的不同主题。实验2特别关注时域离散系统的响应及其验证时域卷积定理。实验内容包括设计和分析不同的离散系统，并利用MATLAB进行图形绘制和信号处理。" 在MATLAB中进行数字信号处理时，实验2主要涉及以下几个关键知识点： 1. **MATLAB编程基础**：实验要求学生熟悉并掌握MATLAB的使用，包括基本的编程语法和函数调用。这包括但不限于变量定义、数组操作、函数调用等。 2. **时域离散系统**：离散系统是指在时间上离散的信号处理系统，通常用于数字信号处理。在这个实验中，学生将学习如何描述和分析离散系统的时域特性。 3. **时域卷积定理**：卷积是信号处理中的核心概念，用于计算一个系统对输入信号的响应。时域卷积定理表明，两个有限长度序列的卷积在离散时间域内可以通过逐项乘法和累加得到。 4. **MATLAB函数应用**： - **conv函数**：用于计算两个序列的卷积。在实验中，它用于计算输入信号与系统响应的卷积，以得到输出信号。 - **DFT函数**：离散傅里叶变换(DFT)是将信号从时域转换到频域的关键工具。在实验中，自定义的DFT函数用于计算数字信号的频谱。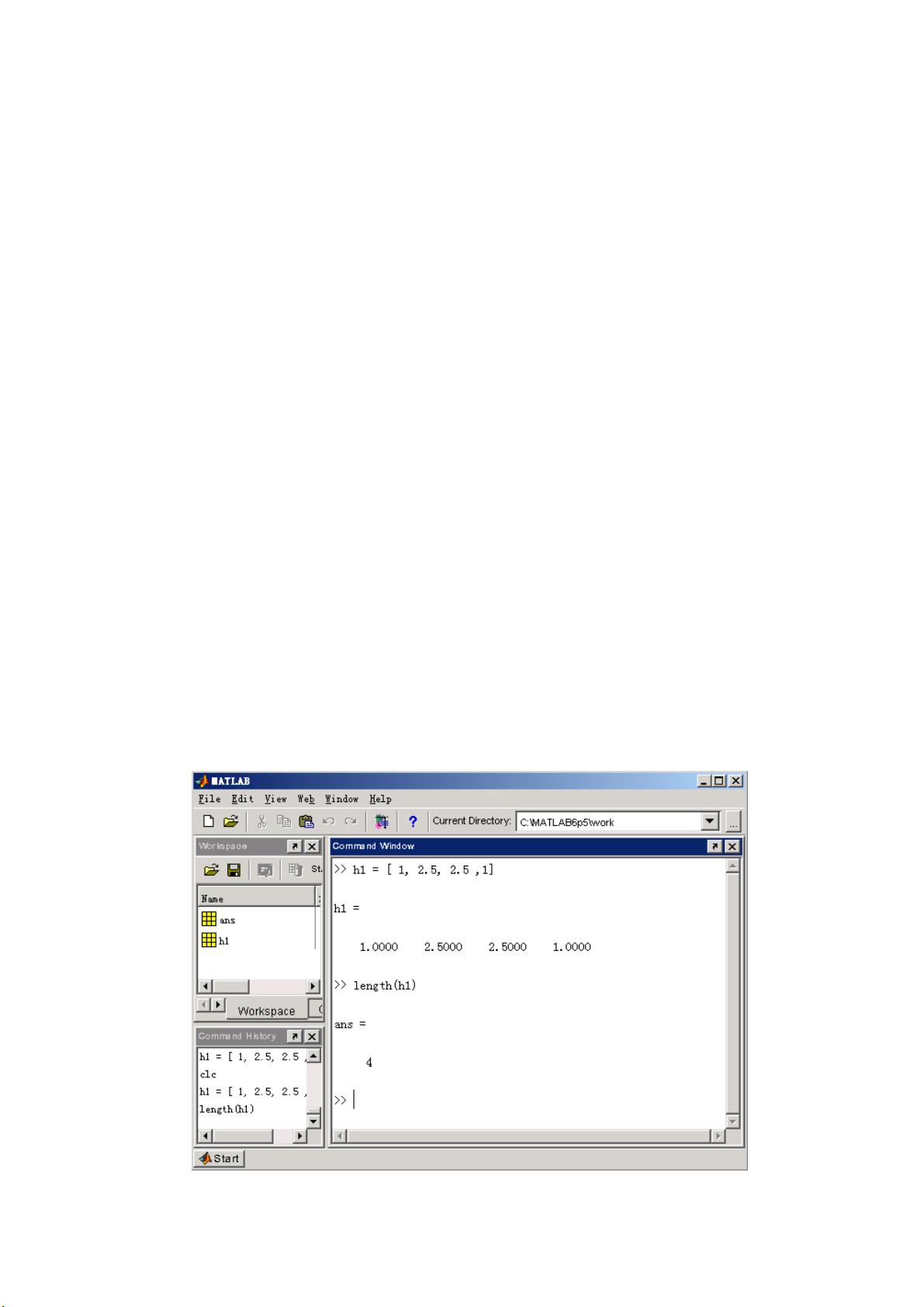 5. **矢量操作**：MATLAB中，矢量的创建和操作是常见的任务。例如，通过数组初始化语法`h1=[1, 2.5, 2.5, 1]`来定义单位抽样响应。同时，`length`函数用于获取矢量的长度。 6. **图形绘制**：实验要求使用MATLAB的图形功能来展示输入、系统和输出信号的时域和频域图形。这通常通过`plot`函数和其他相关图形函数实现，如`figure`函数用于创建新的图形窗口。 7. **数字信号表示**：输入信号和系统响应分别用不同的函数形式表示，如δ函数（单位阶跃函数）和R函数。 8. **频域分析**：通过比较DFT结果验证时域卷积定理，即频域的乘积对应于时域的卷积。这涉及到对离散信号进行傅里叶变换，然后比较不同信号的频谱。 9. **M文件命名规则**：MATLAB的脚本或函数文件应遵循特定的命名规则，不能全由数字组成，且必须以字母开头，可以包含字母、数字和下划线。 这些实验旨在提高学生的MATLAB技能，深化对数字信号处理理论的理解，并通过实际操作加强其在实际问题中的应用能力。通过这样的实验，学生能够更好地掌握数字滤波器设计、谱分析等关键概念。