雷达与笛卡尔坐标系间的插值转换算法详解

本文主要探讨了雷达坐标系与笛卡尔坐标系之间的插值转换方法，涉及到径向插值、方位插值以及高度插值。在实际应用中，这两种坐标系的转换是雷达数据处理和三维空间定位的关键步骤。 在雷达坐标系中，一个点通常由径向距离 \( R \)、方位角 \( A \) 和高度 \( E \) 描述，记为 \( pradar(R, A, E) \)。而在笛卡尔坐标系中，点的位置由 \( x \)、\( y \) 和 \( z \) 坐标表示，记为 \( p3d(x, y, z) \)。转换过程涉及对 \( R \)、\( A \) 和 \( E \) 进行适当的插值，以精确地映射到笛卡尔坐标系。 首先，径向插值 \( R \) 是基于雷达测量的距离，需要在不同的雷达采样点之间进行线性或更复杂的插值。例如，当目标位于两个雷达采样点之间时，通过线性插值计算出中间点的精确径向距离。 方位插值 \( A \) 则涉及到角度的处理。方位角可以表示为 \( A = 0 \)（正北）、\( A = \frac{\pi}{2} \)（正东）等，或者根据 \( x \) 和 \( y \) 的比值通过反正切函数 \( A = atan(\frac{x}{y}) \) 计算。方位插值可能需要考虑角度的周期性，例如，当 \( A \) 超过 \( 2\pi \) 或小于 \( -\pi \)，需要将其调整到正确范围内。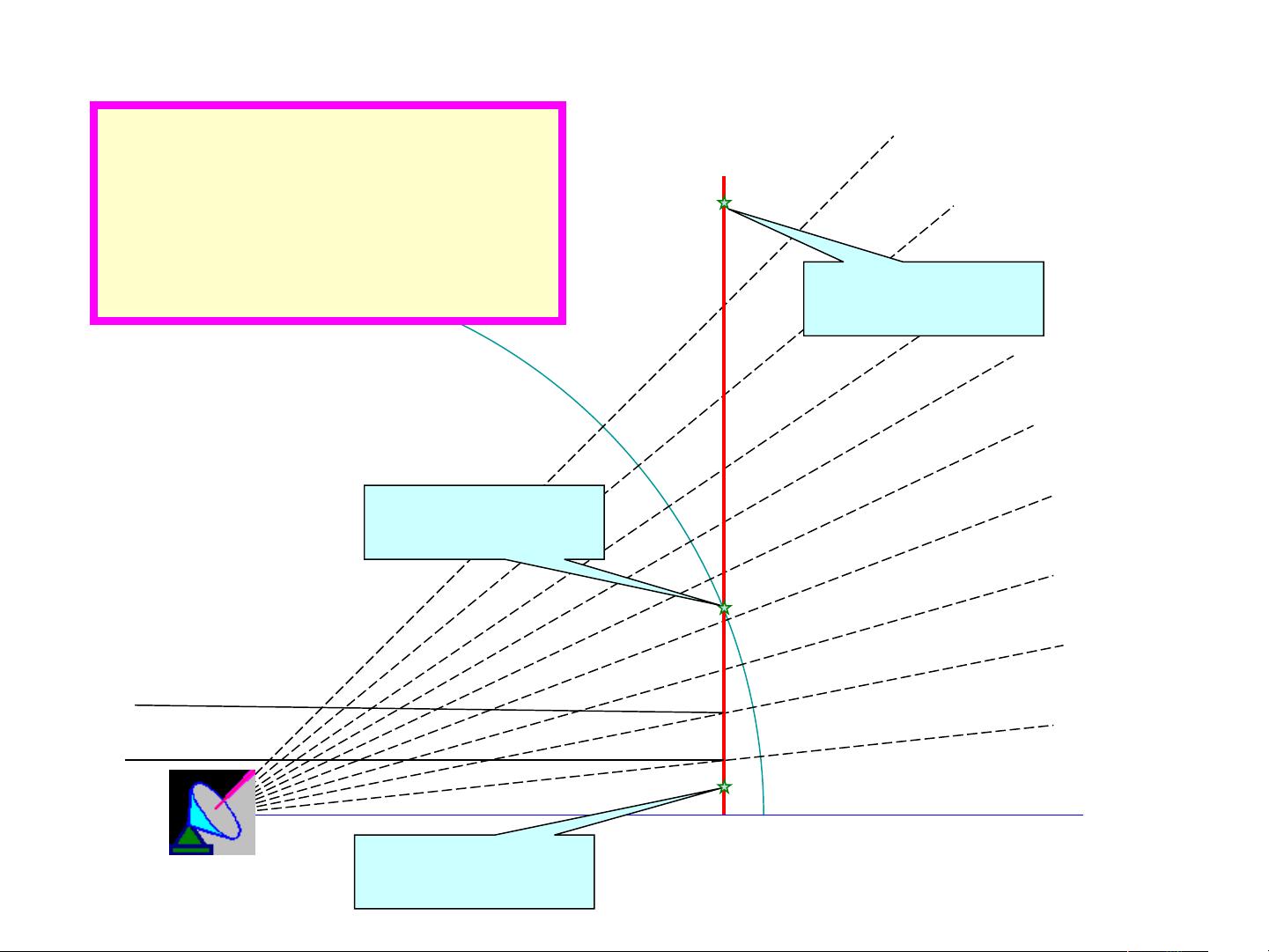 高度插值 \( E \) 是相对于雷达天线的垂直高度。在处理雷达扫描数据时，高度插值可能涉及到不同高度层的投影。如文中所示，插值点被分为三类：第一类在扫描线之下，第二类在扫描线之中，第三类在扫描线之上。对于不同类别的插值点，可能采用不同的插值策略。例如，第二类插值点可能采用线性插值，而第三类可能需要考虑到雷达扫描范围的限制。 在插值过程中，关键参数包括 \( R_{low}, A_{low}, E_{low} \) 和 \( R_{up}, A_{up}, E_{up} \)，分别代表当前点的下限和上限。通过 \( R_{XY} \) 表示 \( R \) 在 \( x-y \) 平面上的投影，\( Z \) 代表垂直高度。插值算法会根据 \( R \) 和 \( E \) 的值计算对应的 \( z_{lowE} \) 和 \( z_{upE} \)，然后结合 \( R \) 的步长 \( dRstep \) 进行高度插值。 雷达坐标系与笛卡尔坐标系的插值转换是通过精确计算和插值技术来完成的，目的是确保雷达数据能够准确地映射到笛卡尔坐标系统中，这对于雷达跟踪、目标定位和三维重建等应用至关重要。这个过程涉及到对径向距离、方位角和高度的插值处理，每一步都需要精确计算，以减少误差并提高数据精度。