数据结构：递归算法详解与递推转化示例

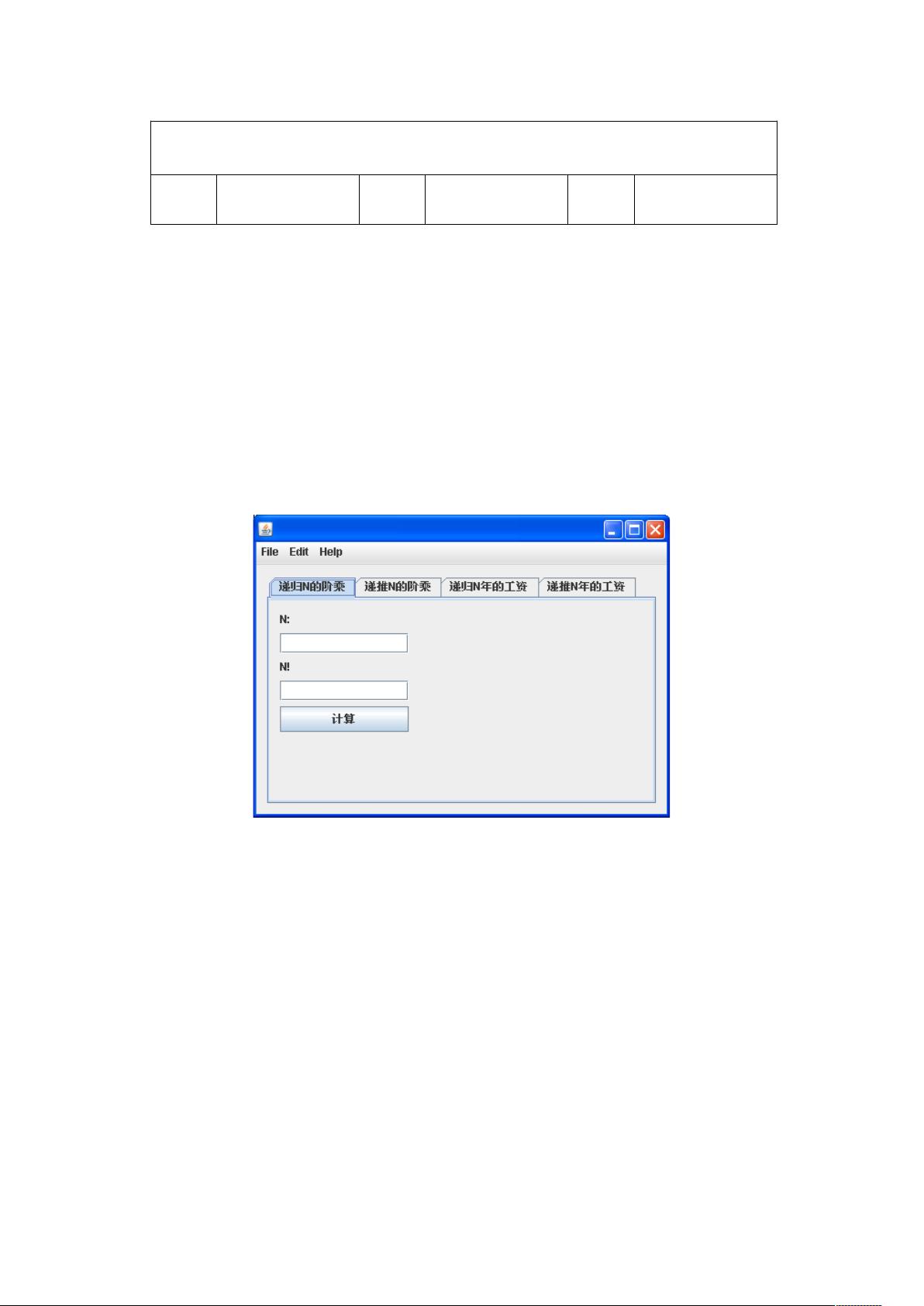
“该资源是关于数据结构中的递归主题，主要用于期末复习，包含了使用MyEclipse实现的递归示例和详细解释。内容涉及如何利用递归计算阶乘，并通过实例展示了递归方法的作用和如何将递归转化为递推过程。” 在数据结构的学习中，递归是一种强大的编程技巧，它允许函数或方法调用自身来解决问题。递归通常用于解决那些可以通过简化规模缩小到相同形式的子问题来解决的复杂问题。在这个资源中，重点是使用递归计算阶乘（N!），这是一个典型的递归应用。 首先，我们来看如何使用递归计算阶乘。阶乘定义为所有小于等于N且大于0的正整数的乘积，即N! = N * (N-1) * ... * 2 * 1。在Java代码中，我们可以创建一个名为`fact1`的方法，如以下所示： ```java public long fact1(long n) { if (n == 0) { return 1; // 0! = 1 } else { long temp = n * fact1(n - 1); // n! = n * (n-1)! System.out.println(temp); return temp; } } ``` 这个`fact1`方法首先检查基础情况，即当n等于0时，返回1（因为0的阶乘定义为1）。对于其他情况，它递归地调用自身，将n乘以前一个数的阶乘（n-1）!，然后返回结果。 递归方法的作用在于它可以将大问题分解为更小的子问题，直到达到一个已知的基础情况。在这个例子中，计算5!会转化为计算4!，然后是3!，依此类推，直到1!，我们知道1!等于1。这种层层分解的过程清晰地展示了递归的工作原理。 接下来，资源中还提到了如何将递归转化为递推。递推是另一种解决问题的方法，它不直接调用自身，而是通过一系列的迭代步骤逐步计算结果。在阶乘的例子中，递推可以使用动态规划来实现，即存储每个子问题的结果，避免重复计算。例如，我们可以创建一个数组来存储已经计算过的阶乘值： ```java public int fact2(int n) { int[] factorial = new int[n + 1]; factorial[0] = 1; for (int i = 1; i <= n; i++) { factorial[i] = i * factorial[i - 1]; } return factorial[n]; } ``` 在这个`fact2`方法中，我们初始化一个数组`factorial`，并先设置0的阶乘为1。然后，通过循环逐个计算每个数的阶乘，利用之前计算出的值（即前一个数的阶乘）来更新当前值。这种方法称为“记忆化”，可以提高效率，特别是对于有重叠子问题的递归算法。 递归和递推都是解决问题的有效工具，各有其适用场景。递归更适合于问题自然具有分治特性的场合，而递推则在需要避免重复计算或优化性能时更有优势。理解这两种方法及其相互转化对于理解和解决数据结构和算法问题至关重要。