2 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 13, NO. 4, APRIL 2004
Reference
signal
Distorted
signal
Quality/
Distortion
Measure
Channel
Decomposition
Error
Normalization
.
.
.
Error
Pooling
Pre-
processing
CSF
Filtering
.
.
.
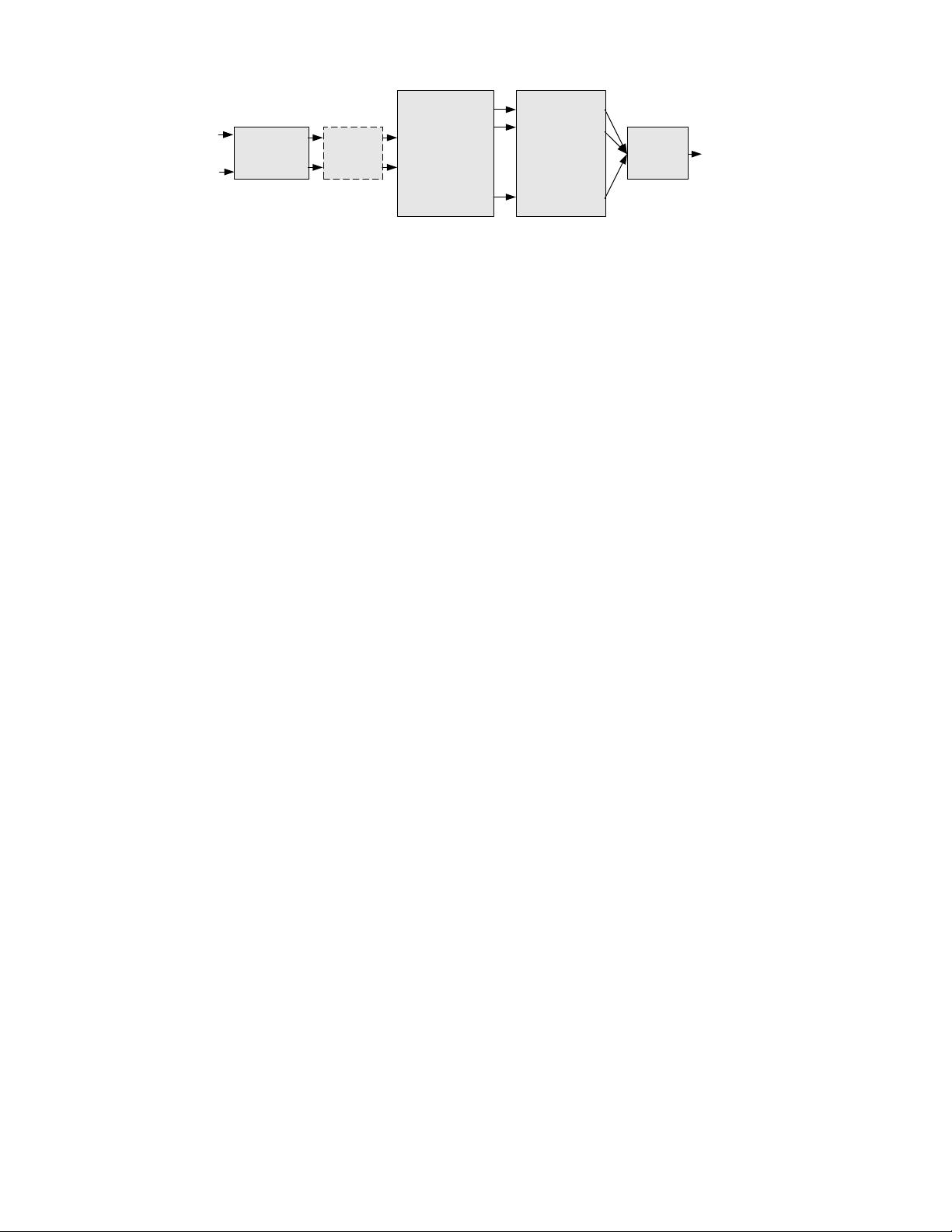
Fig. 1. A prototypical quality assessment system based on error sensitivity. Note that the CSF feature can be implemented either as a
separate stage (as shown) or within “Error Normalization”.
II. Image Quality Assessment Based on Error
Sensitivity
An image signal whose quality is being evaluated can
be thought of as a sum of an undistorted reference signal
and an error signal. A widely adopted assumption is that
the loss of perceptual quality is directly related to the vis-
ibility of the error signal. The simplest implementation
of this concept is the MSE, which objectively quantifies
the strength of the error signal. But two distorted images
with the same MSE may have very different types of errors,
some of which are much more visible than others. Most
perceptual image quality assessment approaches prop osed
in the literature attempt to weight different aspects of the
error signal according to their visibility, as determined by
psychophysical measurements in humans or physiological
measurements in animals. This approach was pioneered
by Mannos and Sakrison [10], and has been extended by
many other researchers over the years. Reviews on image
and video quality assessment algorithms can be found in
[4], [11]–[13].
A. Framework
Fig. 1 illustrates a generic image quality assessment
framework based on error sensitivity. Most perceptual
quality assessment models can be described with a simi-
lar diagram, although they differ in detail. The stages of
the diagram are as follows:
Pre-processing. This stage typically performs a variety
of basic operations to eliminate known distortions from the
images being compared. First, the distorted and reference
signals are properly scaled and aligned. Second, the signal
might be transformed into a color space (e.g., [14]) that is
more appropriate for the HVS. Third, quality assessment
metrics may need to convert the digital pixel values stored
in the computer memory into luminance values of pixels on
the display device through pointwise nonlinear transforma-
tions. Fourth, a low-pass filter simulating the point spread
function of the eye optics may be applied. Finally, the ref-
erence and the distorted images may be modified using a
nonlinear point operation to simulate light adaptation.
CSF Filtering. The contrast sensitivity function (CSF)
describes the sensitivity of the HVS to different spatial and
temporal frequencies that are present in the visual stim-
ulus. Some image quality metrics include a stage that
weights the signal according to this function (typically im-
plemented using a linear filter that approximates the fre-
quency response of the CSF). However, many recent met-
rics choose to implement CSF as a base-sensitivity normal-
ization factor after channel decomp osition.
Channel Decomposition. The images are typically sep-
arated into subbands (commonly called “channels” in the
psychophysics literature) that are selective for spatial and
temporal frequency as well as orientation. While some
quality assessment methods implement sophisticated chan-
nel decompositions that are believed to be closely re-
lated to the neural responses in the primary visual cortex
[2], [15]–[19], many metrics use simpler transforms such as
the discrete cosine transform (DCT) [20], [21] or separa-
ble wavelet transforms [22]–[24]. Channel decompositions
tuned to various temporal frequencies have also been re-
ported for video quality assessment [5], [25].
Error Normalization. The error (difference) between the
decomposed reference and distorted signals in each channel
is calculated and normalized according to a certain masking
model, which takes into account the fact that the presence
of one image component will decrease the visibility of an-
other image component that is proximate in spatial or tem-
poral location, spatial frequency, or orientation. The nor-
malization mechanism weights the error signal in a channel
by a space-varying visibility threshold [26]. The visibility
threshold at each point is calculated based on the energy
of the reference and/or distorted coefficients in a neighbor-
hood (which may include coefficients from within a spatial
neighborhood of the same channel as well as other chan-
nels) and the base-sensitivity for that channel. The normal-
ization process is intended to convert the error into units of
just noticeable difference (JND). Some methods also con-
sider the effect of contrast resp onse saturation (e.g., [2]).
Error Pooling. The final stage of all quality metrics must
combine the normalized error signals over the spatial extent
of the image, and across the different channels, into a single
value. For most quality assessment methods, pooling takes
the form of a Minkowski norm:
E ({e
l,k
}) =
Ã
X
l
X
k
|e
l,k
|
β
!
1/β
(1)
where e
l,k
is the normalized error of the k-th coefficient in
the l-th channel, and β is a constant exponent typically
chosen to lie between 1 and 4. Minkowski pooling may be
performed over space (index k) and then over frequency
(index l ), or vice-versa, with some non-linearity between
them, or possibly with different exponents β. A spatial









