傅里叶变换快速入门：一天掌握基础

"一天征服傅里叶变换.pdf 是一本讲解傅里叶变换的教程，通过简洁易懂的方式介绍这一复杂的概念，特别适合对信号处理感兴趣的读者。尽管标题夸张，但作者承认深入掌握傅里叶变换需要时间和实践，不过教程旨在提供傅立叶变换基础知识，尤其是如何在信号处理中应用。教程采用非传统方法简化傅立叶变换的学习，仅涉及加法和乘法的数学计算。教程分为六个部分，首先会介绍四个基础前提。" 傅里叶变换是一种强大的数学工具，广泛应用于信号分析、图像处理、通信工程等多个领域。它能够将复杂的时域信号转换到频域，揭示信号的频率成分和特性。在信号处理中，傅里叶变换可以帮助我们理解和分离信号中的不同频率成分，对于噪声过滤、频谱分析、调制解调等具有重要意义。 在傅里叶变换的学习过程中，首先需要理解以下几个基本概念： 1. 函数和信号：傅里叶变换处理的对象通常是时间或空间上的函数，这些函数可以代表物理系统的动态过程，如声音信号或图像数据。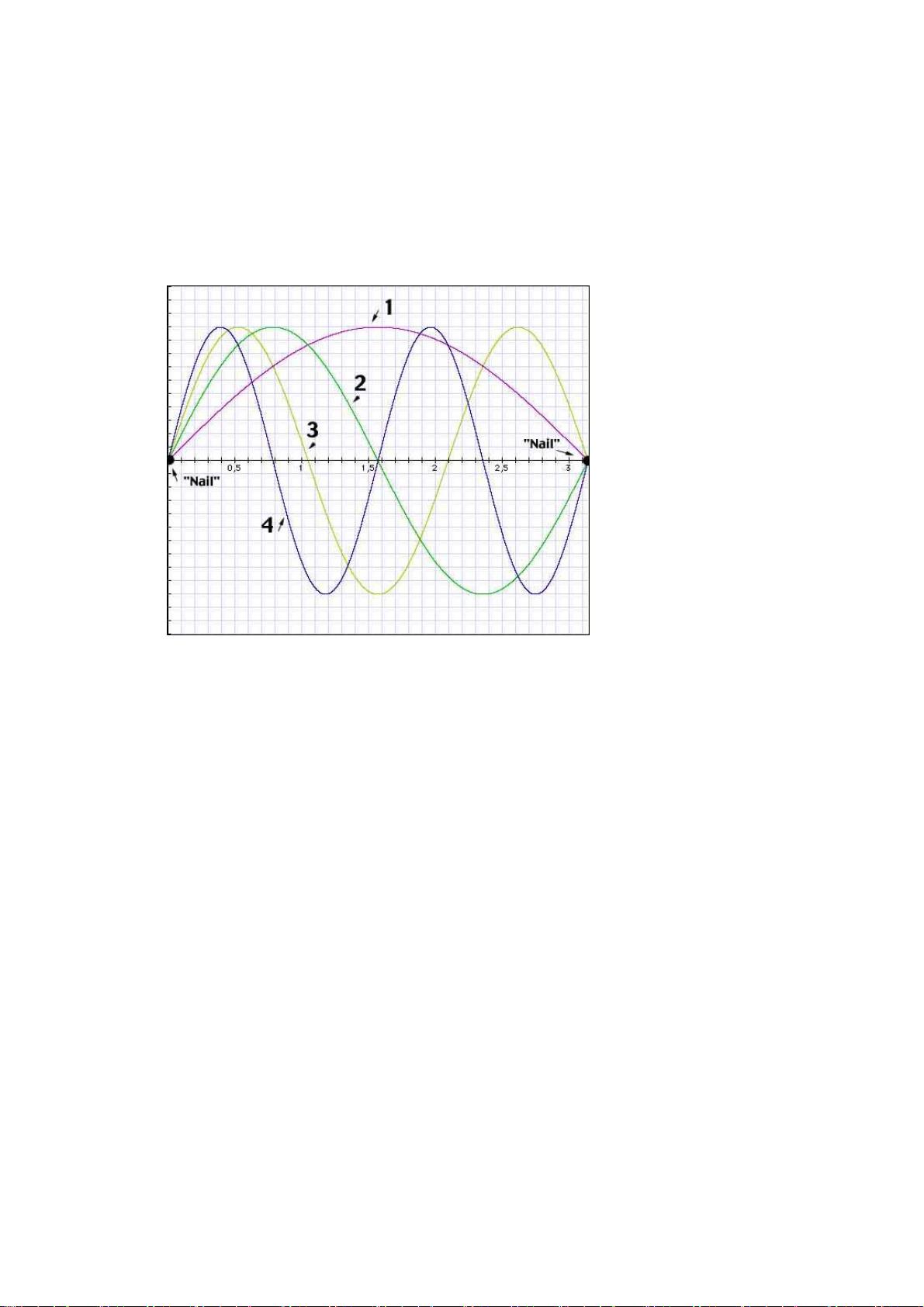 2. 周期性和频率：周期性是傅里叶变换的基础，每个信号都可以分解成不同频率的正弦波之和。频率表示信号变化的速度，单位通常为赫兹（Hz）。 3. 傅里叶级数：在有限区间内的周期函数可以通过傅里叶级数展开，用一组正弦和余弦函数表示。这是傅里叶变换的离散形式，适用于周期性信号。 4. 傅里叶变换公式：傅里叶变换将函数从时域转换到频域，公式通常包括积分运算，对于连续信号；对于离散信号，有离散傅里叶变换（DFT），在数字信号处理中常用快速傅里叶变换（FFT）算法进行计算，大大提高了效率。 教程中提到，通过一种非传统的方法，使得傅里叶变换的学习变得更加直观，不再需要复杂的数学技巧，仅依赖于加法和乘法。这对于初学者来说是个友好的切入点，有助于快速掌握傅立叶变换的核心思想。 在实际应用中，傅里叶变换的六部分可能包括信号的预处理、傅里叶变换的计算、频谱分析、逆傅里叶变换回到时域、频域滤波以及特定领域的应用案例。通过这样的结构，读者可以逐步理解傅里叶变换如何在实际问题中发挥效用，例如在音频编辑中去除噪声，或者在图像处理中进行频域滤波。 "一天征服傅里叶变换.pdf" 提供了一个简明易懂的学习路径，旨在帮助读者快速掌握傅里叶变换的基本原理和实际应用，虽然不能在短时间内精通所有细节，但至少可以建立起对傅里叶变换的初步认识，并为进一步深入学习打下坚实基础。