理解加密与认证：对称-非对称加密、CA认证及K8S证书解析

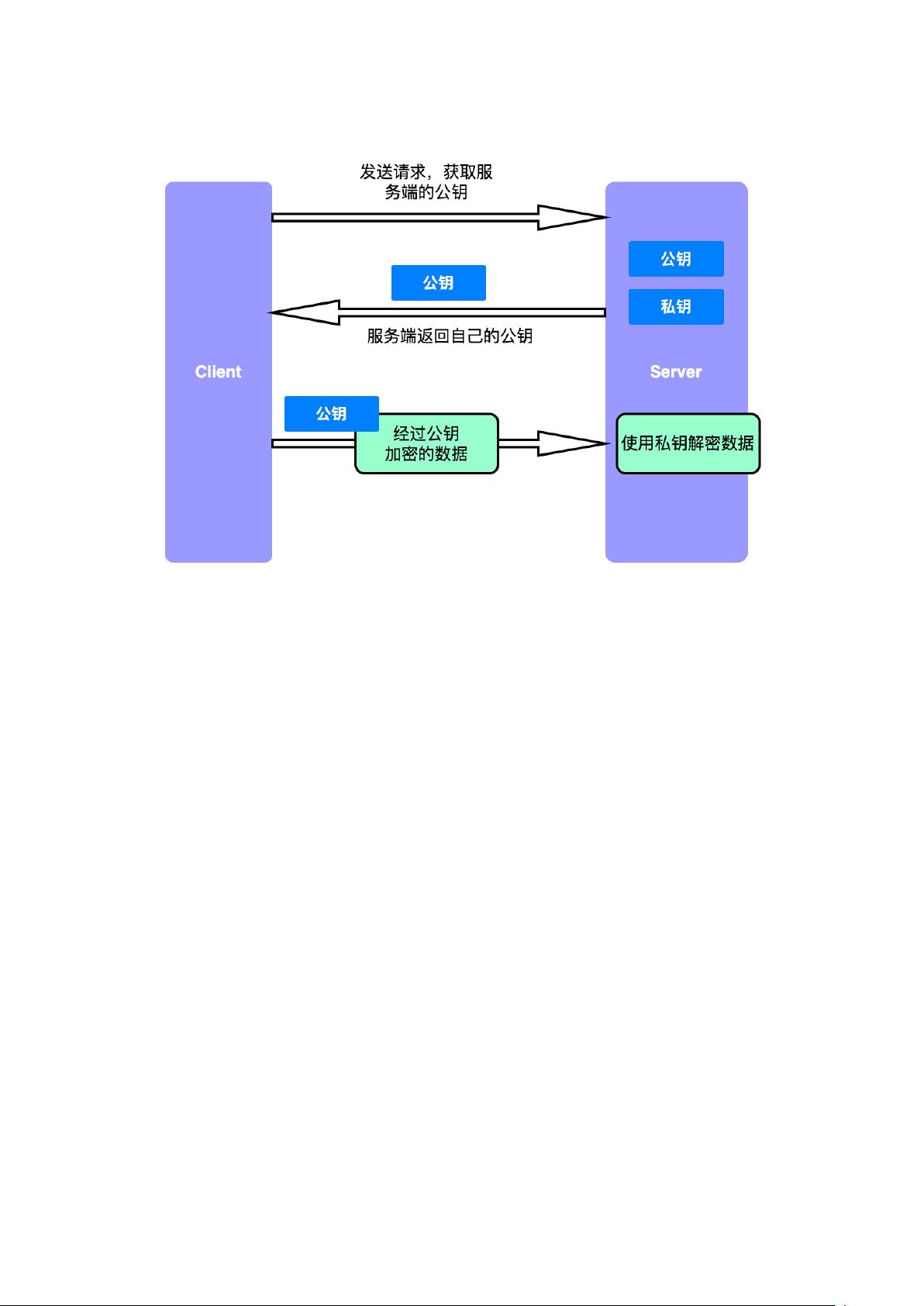
"本文档通过十二张图详细介绍了对称加密、非对称加密的基本概念、优缺点，以及如何结合使用以提高安全性。此外，还探讨了CA（证书权威机构）在HTTPS中的作用，并简要触及Kubernetes（K8S）中证书的应用场景。" 一、对称加密 对称加密是一种基础的加密方式，其核心是通信双方使用相同的密钥进行数据加密和解密。在实际操作中，通常会加入一个盐（salt）作为额外的保护，以增加破解的难度。然而，这种方法的弱点在于密钥的管理和分发，如果密钥被泄露，所有使用该密钥的数据都将暴露。 二、对称加密的不安全性 当对称密钥被黑客获取，或者盐值被滥用时，数据的安全性将受到严重威胁。攻击者能够轻易地解密和篡改数据，使得通信的完整性和保密性无法得到保障。 三、非对称加密 非对称加密使用一对密钥，即公钥和私钥，其中公钥用于加密，私钥用于解密。这种方式的优点在于，即使公钥被公开，私钥仍能保持秘密，从而提高了安全性。然而，仅依赖非对称加密也有其局限性，如数据的传输效率较低且私钥的保护至关重要。 四、非对称加密的不安全性 非对称加密的一个潜在风险是，如果服务端使用公钥发送数据，任何人都能获取并解密，这显然不符合安全需求。因此，非对称加密通常用于在通信双方之间建立一个安全的通道，而非直接加密大量数据。 五、对称加密与非对称加密的结合 为克服各自缺点，两种加密方式常被结合起来使用。具体做法是，客户端通过非对称加密（公钥）获取服务端的随机密钥A，只有服务端的私钥能解密。之后，双方使用这个共享的对称密钥A进行后续的对称加密通信，以提高效率和安全性。 六、对称加密与非对称加密结合的不安全性 尽管这种结合策略提高了安全性，但仍有风险，例如中间人攻击，攻击者可能在密钥交换阶段拦截并篡改随机密钥A，从而破坏整个加密体系。 七、HTTPS与CA认证 HTTPS协议是HTTP与SSL/TLS协议的结合，其中使用了非对称加密来保证连接的安全性。CA（证书权威机构）在其中扮演关键角色，它们为网站颁发经过验证的数字证书，确保用户与正确且可信的服务器建立连接。 八、K8S中的证书应用 在Kubernetes（K8S）集群中，证书广泛用于组件间的身份验证和授权，比如kubelet与apiserver的通信、kube-apiserver之间的相互认证等。证书的管理是K8S安全架构的重要组成部分，确保了服务之间的安全通信。 总结： 通过对称和非对称加密的理解，以及CA认证的作用，我们可以更好地掌握网络通信中的数据安全策略。在实际应用中，需要结合多种安全机制，如证书管理、密钥交换等，以抵御各种网络安全威胁。对于K8S这样的分布式系统，证书管理更是不可或缺，确保了服务的可靠性和安全性。