503 Page 4 of 19 Eur. Phys. J. C (2019) 79 :503
This partial differential equation should be solved according
to the following boundary conditions
∂ρ
∂θ
(z, 0) = 0, (3.7)
ρ(z,) = H. (3.8)
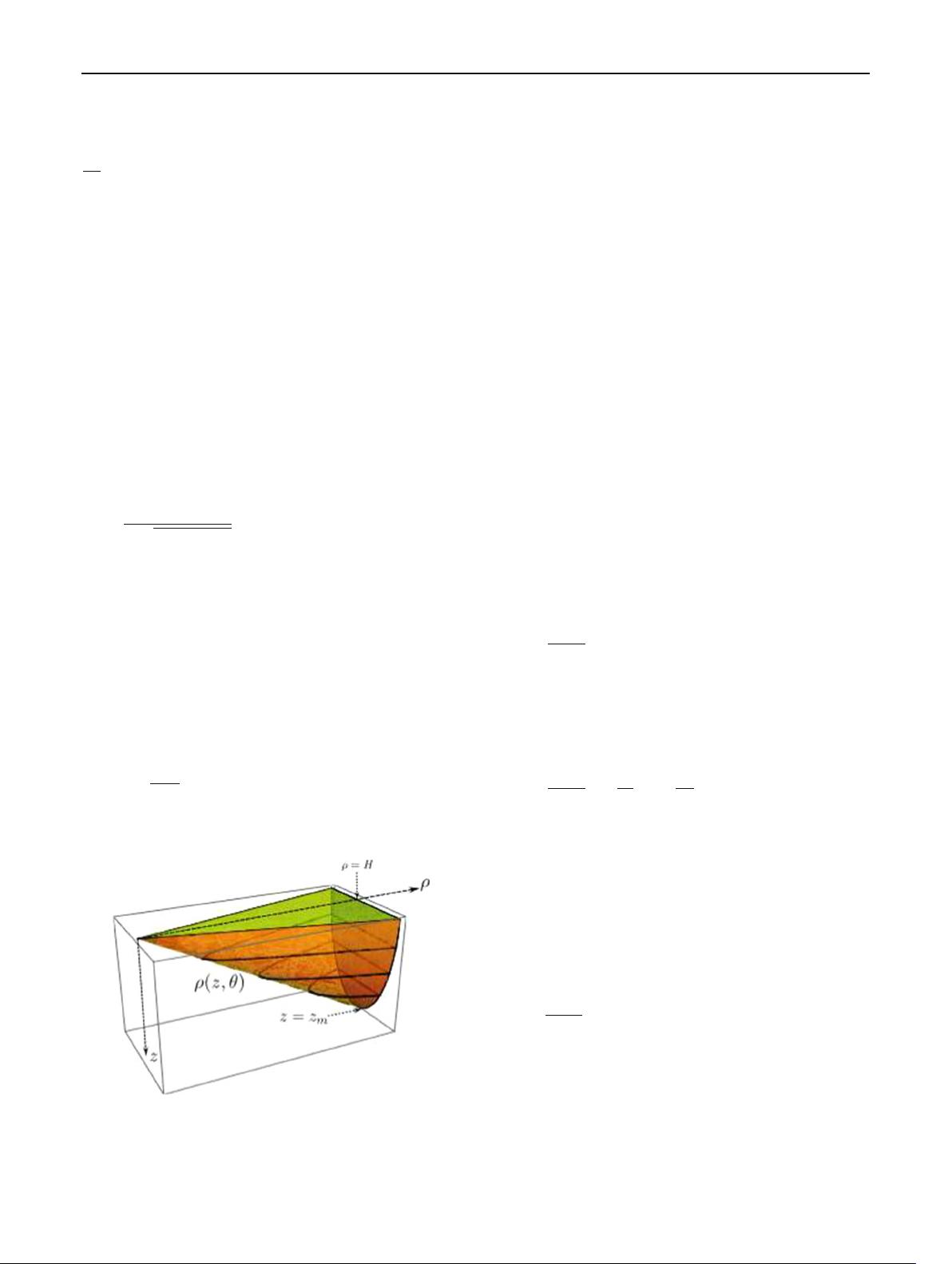
Equation (3.7) shows that at arbitrary z the coordinate ρ on
RT surface acquires its minimum value at θ = 0, while Eq.
(3.8) shows that at the limiting points θ =± the RT surface
touches the boundary ρ = H . See Fig. 1 to get a geometrical
feeling about the problem. To solve Eq. (3.6) we consider a
perturbative ensatz where in the limit μ → 0, we assume
ρ = z/ h(θ). This leads to the following equation for h(θ )
2 +3h
2
+ h
4
+ 2
˙
h
2
+ h(1 + h
2
)
¨
h = 0, (3.9)
In fact, since the resulting Lagrangian does not contain the
variable θ explicitly, the corresponding Hamiltonian, i.e.
K
3
=
(1 + h
2
)
h
2
1 + h
2
+
˙
h
2
. (3.10)
is constant. Therefore Eq. (3.10) with K
3
as a constant can be
considered as the first integration of Eq. (3.9). The boundary
condition (3.7)gives
˙
h(0) = 0 at the turning point θ = 0.
Hence, the constant K
3
can be written in terms of h
0
= h(0).
In principal the Eq. (3.9) can be solved to find the function
h(θ ). However, we use this equation to find
˙
h as a function
of h. Inserting these results in Eq. (3.6), one can find the
entanglement entropy of kink [13]. Then we can complete
our enzatz by considering the following expansion
ρ(z,θ) =
z
h(θ )
+ μ
2α
z
2α+1
g
2
(θ) +···. (3.11)
Fig. 1 Schematic figure of the RT extension of the kink (green region)
into the bulk [13]
Inserting the complete ansatz (3.11) into the equation of
motion (3.6) we find (in addition to Eq. (3.9)) the follow-
ing equations for g
2
,
2h
3
(1 + h
2
)(1 + h
2
+
˙
h
2
) ¨g
2
+ 2h
2
˙
h(2(5 + 2h
2
+ 2α)
˙
h
2
+ (1 + h
2
)(10 +5h
2
+ 4α + h
¨
h)) ˙g
2
− 2h(−2(−2 + h
2
+ α + 2α
2
)
˙
h
4
+
˙
h
2
(22 +h
4
+ 2(7 − 2α)α + h
2
(19 + 4α − 8α
2
)
+ 2h(2 +h
2
+ 2α)
¨
h) + (1 + h
2
)(2(9 +8α)
+ h
2
(19 + 4h
2
− 4(−2 + α)α)
+ 3h(2 + h
2
+ 2α)
¨
h))g
2
+ (2(−1 + α)
˙
h
4
+ (1 + h
2
)(−8 + h
4
+ 2h
2
(−2 +α)
+ h(−2 + h
2
)
¨
h) +
˙
h
2
(h
4
+ 2(−5 +α) + h
2
(−5 + 4α)
+ h(−1 + h
2
)
¨
h)) = 0. (3.12)
As is expected, for the generic problem of the entanglement
entropy, we will find UV divergences in the limit z → 0
or equivalently as ρ → 0 (for arbitrary −<θ <)or
θ → (for finite ρ). In terms of the variable h the latter
limit is equivalent to h → 0. The UV divergent terms of the
entanglement entropy originate from the divergences of the
integrand as well as the limits of the integral Eq. (3.4)as
S|
k
=−
2π L
2
l
2
p
δ
z
m
dz
−
−+
dθ L(ρ, ˙ρ, ρ
), (3.13)
which upon changing the integration limits of θ from
(−, ) to (0,) and replacing dθ in Eq. (3.4)bydh/
˙
h,
reads
S|
k
=−
4π L
2
l
2
p
δ
z
m
dz
z
h
1c
h
0
dh
˙
h
L(ρ,
˙
hdρ/dh,ρ
). (3.14)
Concerning the integral bounds in Eq. (3.14), from the bound-
ary condition (3.8)wehaveρ(z,− (z)) = H ; hence we
can define h
1c
(z) = h( −(z)). In the limit z = δ → 0we
have h
1c
(δ) = h( − (δ)). The limit z
m
is also achieved
via the condition ρ(z
m
, 0) = H . Inserting ρ from Eq. (3.11)
into (3.14) gives the following expansion for the entangle-
ment entropy with respect to μ
S|
k
=−
4π L
2
l
2
p
(I
0
+ μ
2α
I
1
+···), (3.15)
where
I
k
=
δ
z
m
dzz
(2α)k−1
h
1c
h
0
dhG
k
(h), (3.16)
123









