"点积内积与叉积-算法计算几何"

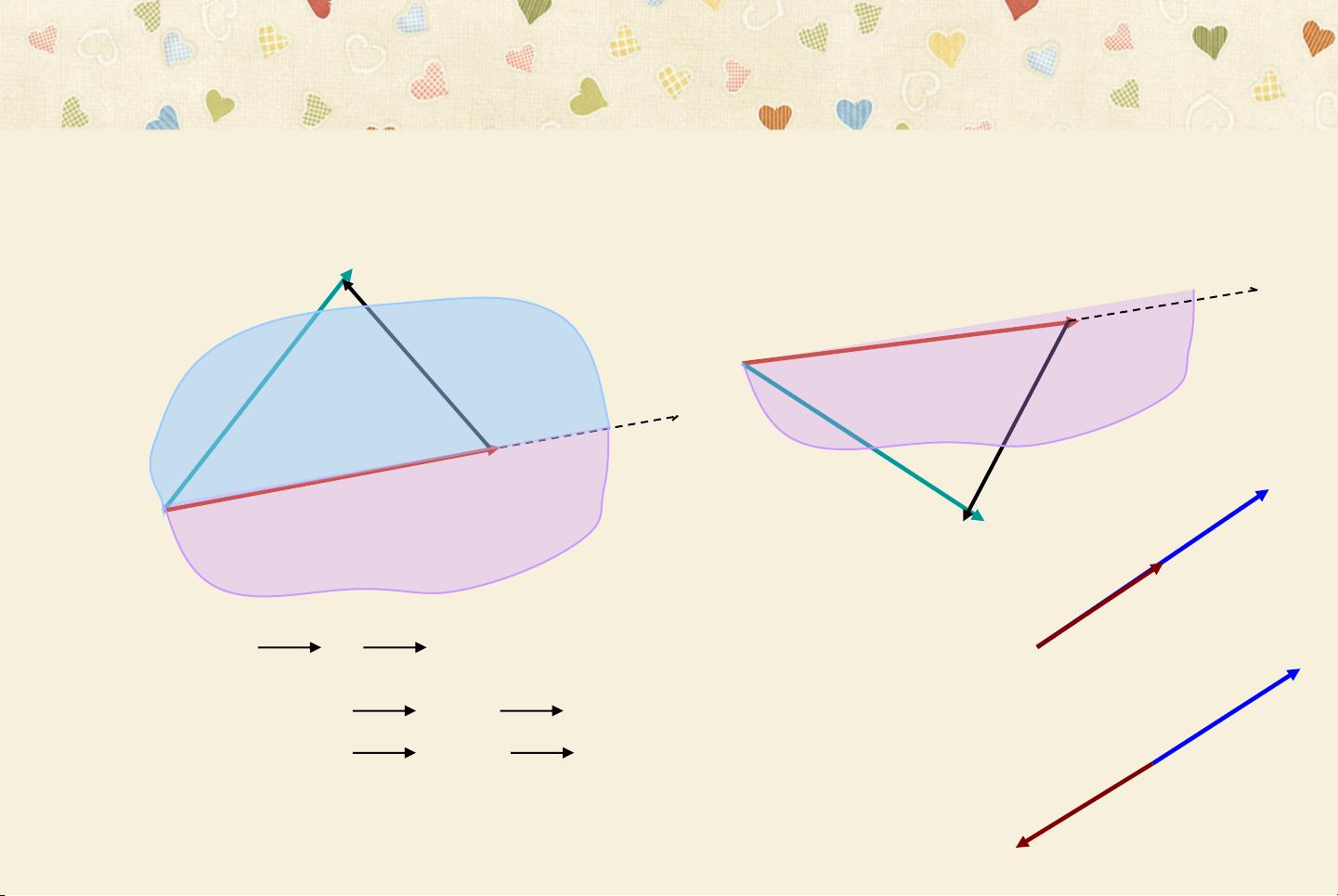
点积内积-计算几何（叉积和点积在算法上应用）；点积（内积）已知有向线段op1=(x1, y1),op2=(x2, y2)op1 与 op2 的点积表示为 op1 · op21. 几何意义：OP1在OP2上的的投影 OP1’与OP2的长度乘积 op1 · op2 = |op2| * |op1| * cos(a)，0<=a<=180,2. P1(x1,y1) P2(x2,y2) O(0,0) P1’ a op1 · op2 = x1x2 y1y2 = op2 · op1; 计算几何学1. 叉积2. 点积计算几何的基本工具计算几何的常见问题总结2叉积（外积）已知有向线段 op1=(x1, y1),op2=(x2, y2)op1与op2叉积表示为：op1×op2几何意义：是以op1、op2为边的平行四边形的有向面积。即 op1×op2 = |op1| * |op2| * sin(a)，0<=a<=180,a是两向量的夹角.op1×op2 = = x1y2 – x2y1 = -(x2y1 – x1y2) = - = - op2×op1p(x1 x2,y1 y2)x1y2y1x2p1(x1,y1)p2(x2,y2)aO(0,0)x2y1y2x13p2(x2,y2)p1(x1,y1)p2(x2,y2)O op1×op2= x1y2 – x2y1性质：a. 若op1×op2 >0，则向量op1到op2成逆时针；即op2在op1的左边。b. 若op1×op2 <0，则向量op1到op2成顺时针；即;" 在计算几何中，点积内积和叉积外积是常用的算法工具。首先，点积（内积）定义了有向线段op1=(x1, y1)和op2=(x2, y2)之间的关系。点积表示为op1 · op2，其几何意义是op1在op2上的投影op1'与op2的长度乘积。可以表示为op1 · op2 = |op2| * |op1| * cos(a)，其中0<=a<=180。通过坐标表示，如果有P1(x1,y1)和P2(x2,y2)，以及原点O(0,0)，那么op1 · op2可以表示为x1x2 + y1y2。点积的性质包括op1 · op2 = op2 · op1，这对于计算几何学中的问题非常有用。 另外，叉积（外积）也是计算几何中常用的工具。叉积表示为op1 × op2，其几何意义是以op1、op2为边的平行四边形的有向面积。可以表示为op1 × op2 = |op1| * |op2| * sin(a)，其中a是两向量的夹角，且0<=a<=180。通过坐标表示，op1 × op2可以表示为x1y2 – x2y1。叉积的性质包括op1 × op2 = - (op2 × op1)，并且如果op1 × op2 >0，则向量op1到op2成逆时针；如果op1 × op2 <0，则向量op1到op2成顺时针。 在算法中，点积和叉积的应用非常广泛。它们可以帮助计算几何学的各种常见问题，如计算线段的交点、判断两条线段是否相交、计算多边形的面积等等。由于点积和叉积具有清晰的几何意义和简单的数学表示，因此它们成为了计算几何学的基本工具之一。 总之，点积内积和叉积外积在计算几何学中起着重要的作用。它们不仅可以帮助解决各种常见问题，还可以在算法中得到应用。通过理解点积和叉积的几何意义和数学表示，我们可以更好地理解和应用它们在计算几何学中。