哈夫曼树：构建与应用详解

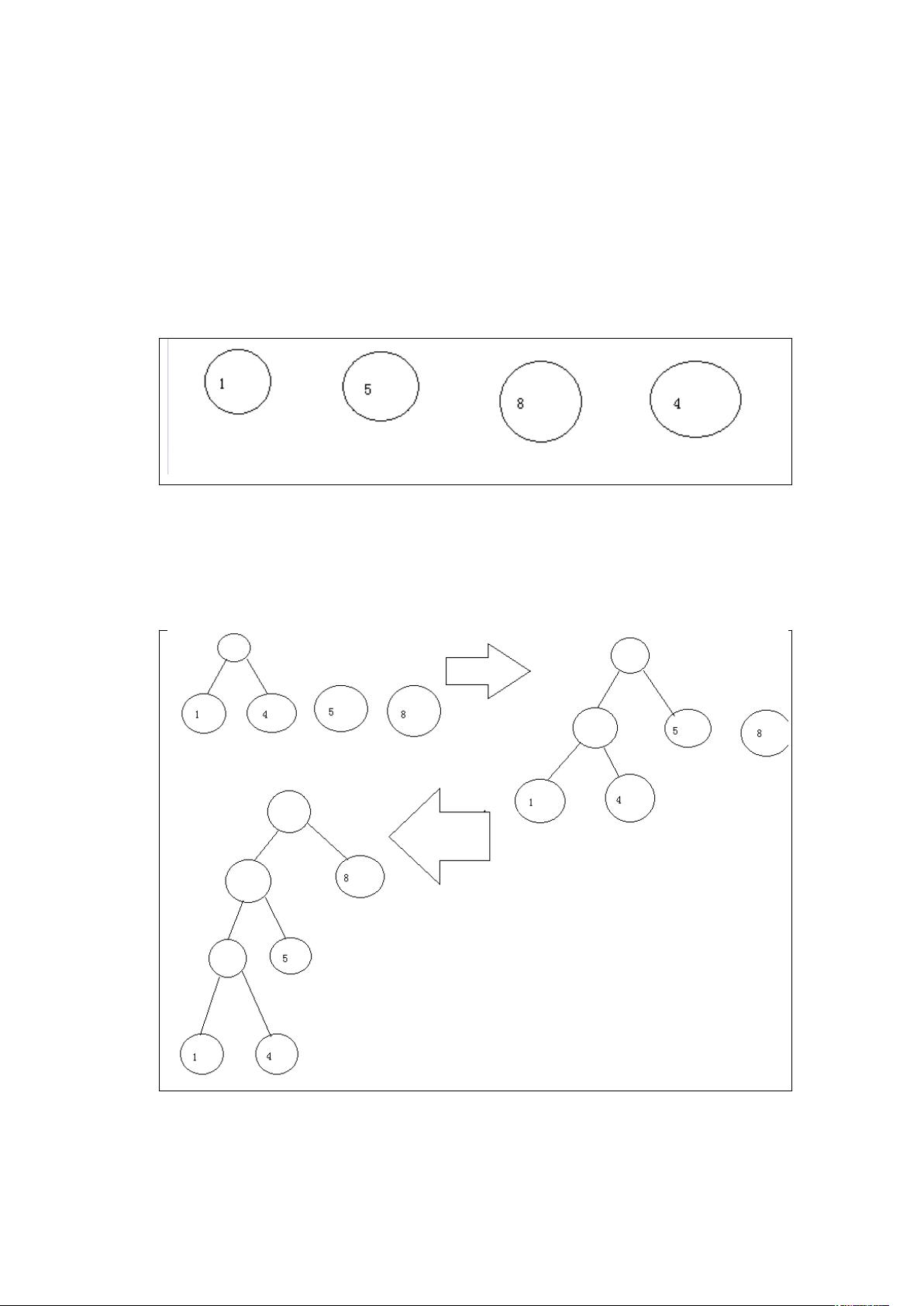
哈夫曼树是一种特殊的二叉树，也称为最优二叉树，主要用于优化带权重信息的数据结构。在给定的描述中，我们了解到以下几个关键知识点： 1. **定义与构建**： - 哈夫曼树是当节点带有权重时，通过构建一棵使得所有边的权重乘以节点度之和最小的二叉树。其构建过程包括： - 将带权重的节点按照权重从小到大排序。 - 选取排序后的前两个节点作为新父节点的子节点。 - 从列表中移除已选择的节点，重复此过程直至所有节点被选完。 - 通过这种构建方式，得到的树不仅结构优雅，而且叶子节点的路径长度具有最优性。 2. **应用场景**： - 哈夫曼树在实际中有多种应用，比如在 Apache 负载均衡中的按权重请求策略，路由器的路由算法，汉字点阵字形压缩存储，以及搜索引擎的快速检索算法等。这些场景的核心是利用权重和距离信息来提高效率或压缩数据。 3. **实现方法**： - 实现哈夫曼树的核心是通过编程实现上述构建过程。在 Java 中，可以使用 `ArrayList` 存储离散节点，`ArrayDeque` 或 `Queue` 类进行节点的进出操作。代码示例展示了一个简单的哈夫曼树构建过程。 ```java import java.util.ArrayList; import java.util.List; import java.util.Queue; public class HuffmanTree { // 哈夫曼树类定义 // ... public static void buildHuffmanTree(List<Node> nodes) { // 排序节点 nodes.sort((n1, n2) -> n1.weight - n2.weight); // 构建过程 while (nodes.size() > 1) { Node left = nodes.remove(0); Node right = nodes.remove(0); Node newNode = new Node(left, right); newNode.weight = left.weight + right.weight; nodes.add(newNode); } // 返回构建完成的根节点 return nodes.get(0); } // 其他辅助方法，如广度优先遍历等 } ``` 这里的 `Node` 类可能包含权重和子节点等属性。构建完成后，可以通过广度优先搜索（BFS）来遍历哈夫曼树并获取最短路径。 总结来说，哈夫曼树是一种数据结构优化工具，用于处理带有权重的节点问题，其核心在于构建过程中的排序和合并操作。在实际应用中，它可以应用于数据压缩、路由优化、信息检索等多个领域，通过 Java 等编程语言的实现，简化了复杂的问题求解。