"数学建模中的曲线拟合与插值方法解析和应用"

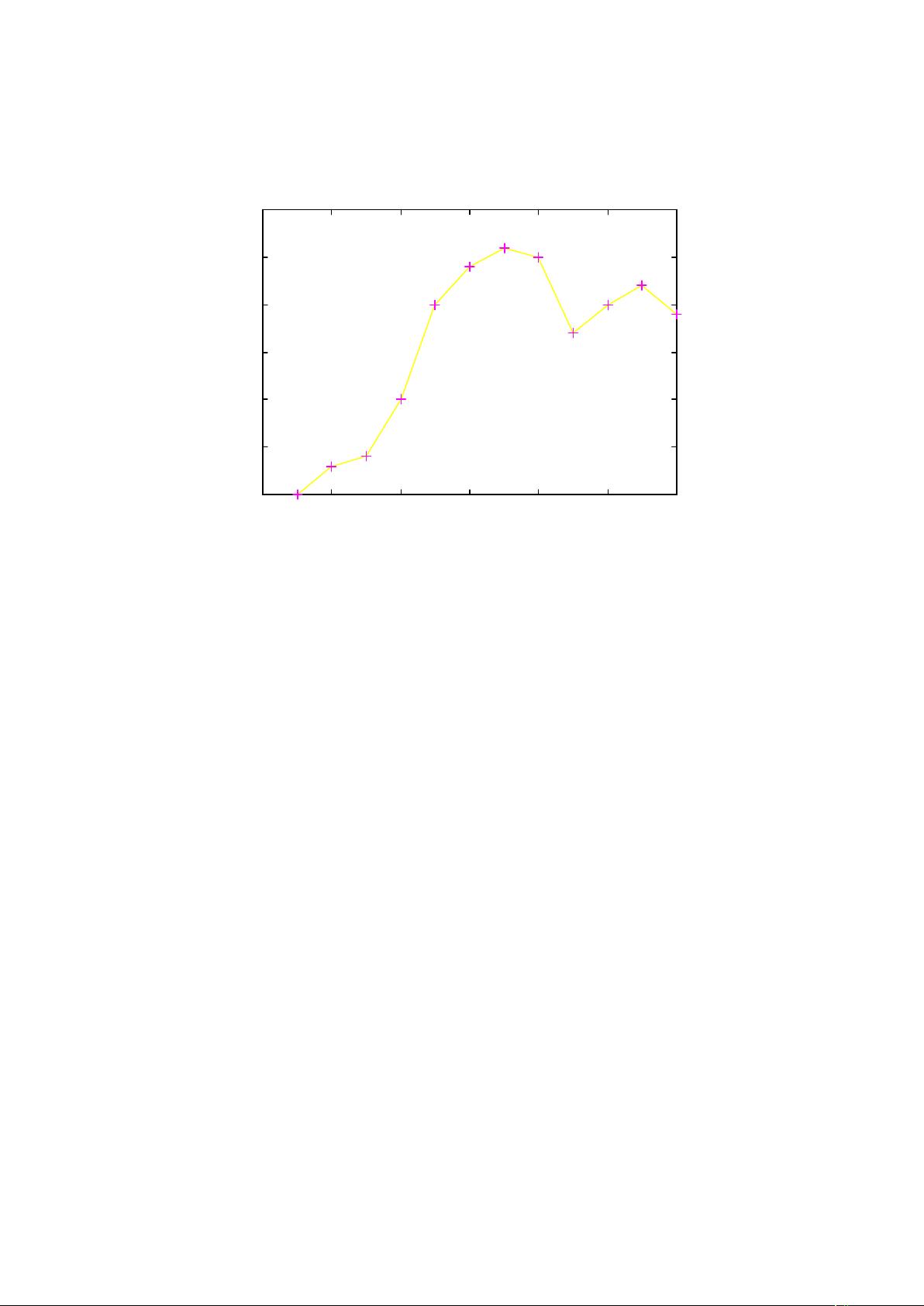
曲线拟合与插值是数学建模中常用的方法，用于描述数据，并解决相关问题。在插值法中，数据被认为是准确的，需要找到描述数据点间关系的方法。而曲线拟合则是寻找一条光滑曲线，最佳地拟合数据，但不必经过每个数据点。曲线拟合涉及回答两个基本问题：最佳拟合意味着什么？应该用什么样的曲线？最佳拟合通常被定义为在数据点的最小误差平方和，而所用的曲线可以是多种多项式。因此，曲线拟合是相当简洁的，并且数学上称为多项式的最小二乘曲线拟合。 曲线拟合与插值在许多应用领域中都有重要的作用，例如在工程、经济学、统计学等领域中都有应用。例如，在工程领域中，曲线拟合与插值可以用于处理传感器数据，从而改善控制系统的性能。在经济学中，它可以用于预测和分析市场趋势，以及指导决策。在统计学中，它可以用于分析样本数据，从而得出总体数据的相关特性。因此，掌握曲线拟合与插值的方法对于解决实际问题非常重要。 在数学建模中，曲线拟合通常涉及选择适当的曲线类型，并使用最小二乘法来确定曲线参数。最小二乘法是一种常见的数学优化方法，通过最小化数据点与拟合曲线之间的误差平方和来确定最佳拟合。在图1.1中，虚线所代表的曲线是使误差平方和尽可能小的曲线，即是最佳拟合。通过数学计算，可以精确地确定最佳拟合的曲线参数，从而描述数据并解决相关问题。 除了最小二乘法外，还有其他曲线拟合与插值的方法，例如样条插值、拉格朗日插值等。这些方法在不同情况下具有各自的优势和局限性，需要根据实际问题选择合适的方法。例如在图像处理中，样条插值方法可以用于图像重构，提高图像分辨率。而在金融学中，拉格朗日插值方法可以用于估计期权定价模型中的隐含波动率。因此，熟练掌握不同的曲线拟合与插值方法对于解决不同领域的实际问题至关重要。 总之，曲线拟合与插值是数学建模中常用的方法，用于描述数据并解决相关问题。通过选择合适的曲线类型和使用最小二乘法等数学方法，可以精确地描述数据并进行相关问题的分析。同时，不同的曲线拟合与插值方法在不同领域具有各自的应用，需要根据实际情况选择合适的方法。掌握曲线拟合与插值的方法对于解决实际问题非常重要，对于提高数学建模的能力和水平具有重要意义。