第05章：线性系统在数字信号处理中的基石

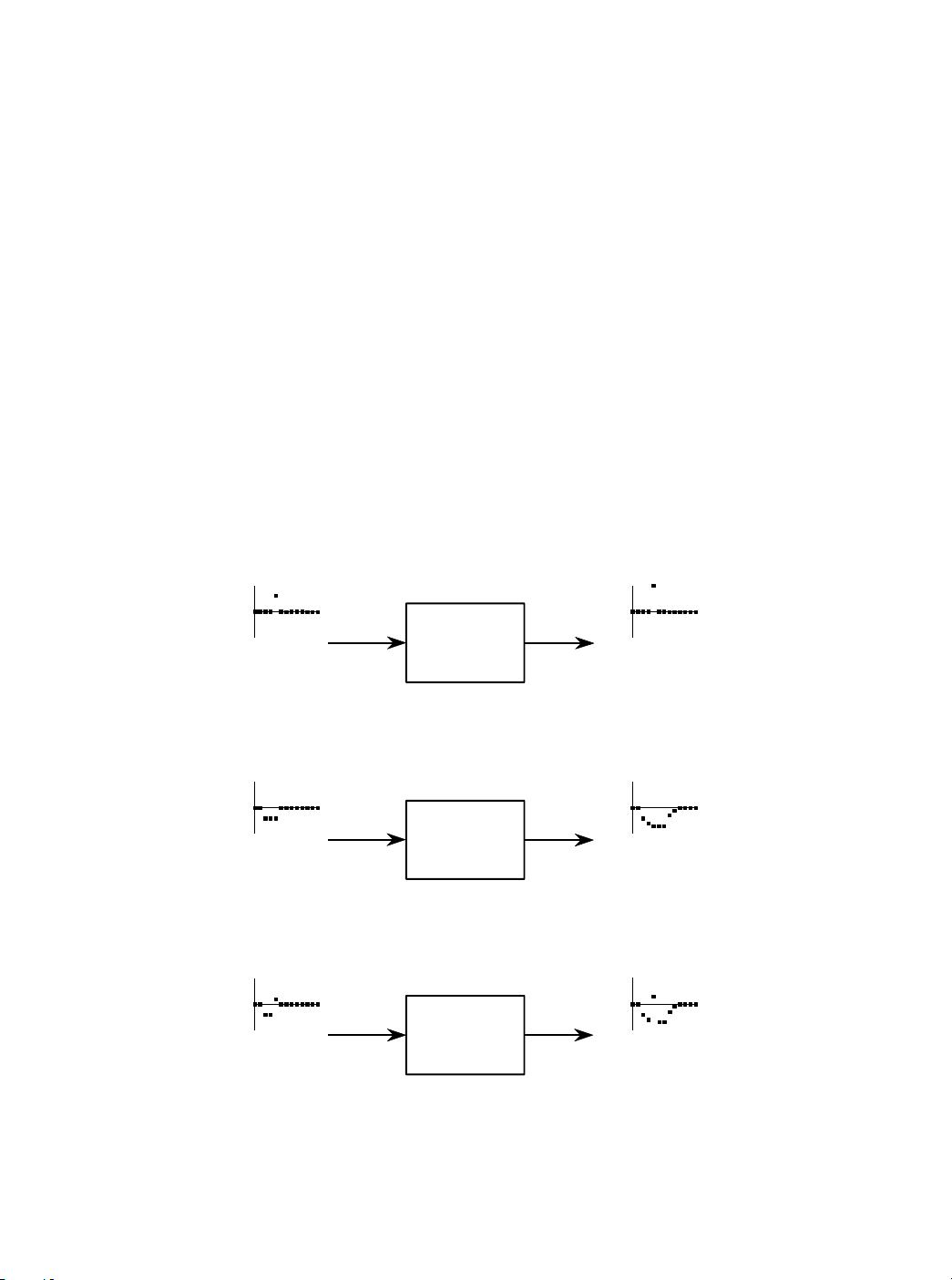
在"The Scientist and Engineer's Guide to Digital Signal Processing"第五章中，讨论了线性系统在数字信号处理(DSP)中的核心地位。这一章节是理解 DSP 技术的基础，因为大多数 DSP 方法都依赖于称为“叠加”的分而治之策略。叠加原理允许复杂信号被分解成简单的组成部分，每个部分独立处理后再合并结果，这样就把一个难题转化为多个易于管理的小问题。 线性系统是指遵循特定数学规则的系统，它们的行为满足加法和比例法则，即输入信号的线性组合会产生与之对应的输出的线性组合。在工程和科学研究中，许多实际应用都符合线性系统的特性，因此线性系统理论在信号处理领域具有广泛的应用价值。 信号和系统是紧密相关的概念。信号可以看作是一个参数随另一个参数变化的描述，如电子电路中电压随时间的变化，或者图像中亮度随距离的变化。系统则是对输入信号进行处理并产生相应输出的设备或过程。例如，图5-1中的块图展示了输入信号（比如声音或图像）如何通过系统转化为输出信号（比如音频播放或图像处理后的输出图像）。 在本章中，首先定义了什么是线性系统，包括其基本性质。接着，探讨了如何利用线性系统的特性来分析和设计信号处理器。一种常用的方法是将复杂的连续信号分解为简单的波形，如正弦或余弦函数，通过傅里叶变换等技术实现频域处理。通过这样的分解，可以有效地滤波、放大、延迟或压缩信号，这些都是 DSP 中广泛应用的信号处理技术。 此外，线性系统还涉及系统函数和系统矩阵的概念，它们是描述系统行为的重要工具。系统函数表示输入信号到输出信号的映射关系，而系统矩阵则用于表示线性系统在复数域中的行为。通过研究这些概念，工程师能够更好地理解线性系统如何处理不同类型的输入，并设计出适应特定需求的信号处理算法。 第五章深入浅出地介绍了线性系统在 DSP 中的重要性，不仅涵盖了线性系统的基本概念，还涵盖了信号分解、叠加原理以及各种信号处理技术的应用。理解这一章的内容对于任何从事 DSP 工程的人员来说都是至关重要的，因为它为后续的滤波器设计、调制解调、频谱分析等高级 DSP 技术打下了坚实的基础。