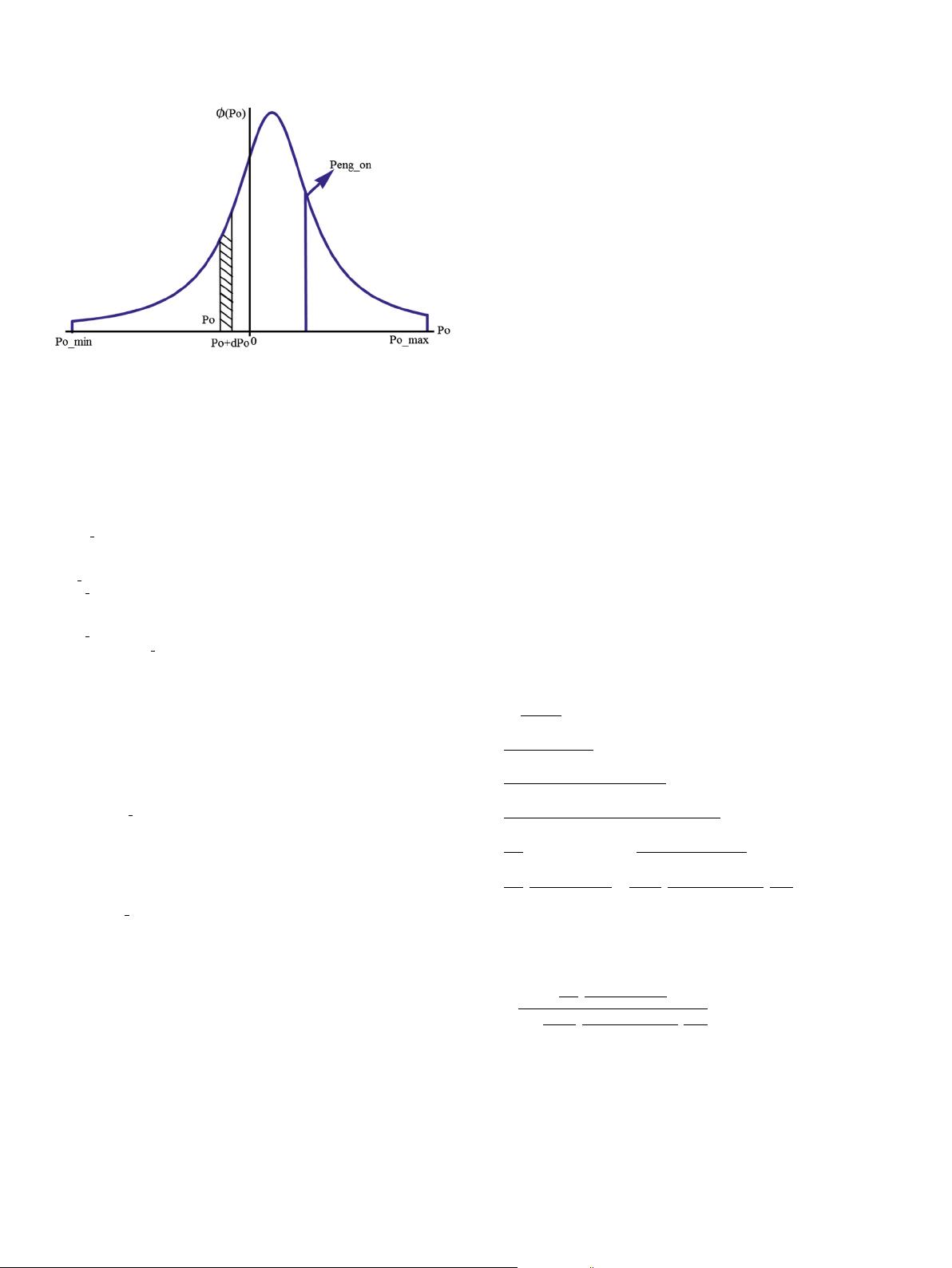
Suppose the total trip duration is t_total, and the power
threshold at which the engine is turned on is P
eng_on
, as shown in
Fig. 2. It means that when the driveline power is less than P
eng_on
,
the vehicle is powered by the battery only, and when the driveline
power is more than P
eng_on
, the engine will be turned on and the
vehicle is powered by the engine and battery together. Now, we can
easily get,
8
>
>
>
>
>
>
>
>
>
>
<
>
>
>
>
>
>
>
>
>
>
:
Z
P
eng on
P
o min
F
ð
P
o
Þ
dP
o
¼ t
off
Engine off
Z
P
o max
P
eng on
F
ðP
o
ÞdP
o
¼ t
on
Engine on
t
off
þ t
on
¼ t total
(3)
where P
o
is the driveline power,
F
(P
o
) represents the ratio of a
whole trip duration when the driveline power is within the interval
P
o
and P
o
þ dP
o
, P
o_min
and P
o_max
are the minimum and maximum
driveline power, t
off
and t
on
are the engine off and on duration
respectively. From this point, how to determine the optimal P
eng_on
becomes very critical, which can influence the engine-on time and
thus influence the fuel-consumption. Based on Eq. (3), we can get,
8
>
>
>
>
>
>
>
>
>
>
<
>
>
>
>
>
>
>
>
>
>
:
D
1
¼
Z
P
eng on
P
min
IðP
o
Þ
F
ðP
o
ÞdP
o
D
2
¼
Z
P
max
P
eng on
IðP
o
Þ
F
ðP
o
ÞdP
o
D
1
þ
D
2
¼ C$
D
SOC
(4)
where
D
1
and
D
2
are the SOC variation when engine is off and on, I
is the battery current, C is the battery capacity,
D
SOC is the SOC
difference between the ending value and the initial value. In the
paper, the ending SOC is set to 30%, so we can get
D
SOC˛½ 0 70% (5)
According to Eq. (4), P
eng_on
can determine
D
1
and
D
2
, however,
it cannot determine the battery current when the engine is on. As
shown in Fig. 3, we need to determine the battery current (battery
power) when the engine is on.
Based on the above discussion, the fuel-consumption can be
influenced by the engine-on power threshold and the battery cur-
rent when the engine is on. Therefore, the engine-on power
threshold should be determined and the relationship between the
engine fuel-rate and battery current should be built. Hence, the
vehicle powertrain needs to be analyzed in detail first.
2.2. Vehicle powertrain analysis
The powertrain structure of the power-split PHEV analyzed in
the paper is shown in Fig. 4. It consists of a gasoline ICE, a lithium-
ion battery pack, two electric motors, and a planetary gear set
which connects the motor, engine, and the final driveline together
with a predetermined gear ratio [1,2,9]. Table 1 lists the vehicle
parameters, and Fig. 4 details the powertrain structure.
From Fig. 4, P
o
equals the sum of P
r
and P
mot1
, i.e.,
P
o
¼ T
o
w
o
¼ P
r
þ P
mot1
¼ T
r
w
r
þ T
mot1
w
mot1
(6)
where T
r
, T
o
, and T
mot1
denote the torque of ring gear of the plan-
etary gear set, driveline, and motor 1, w
r
, w
o
, and w
mot1
denote their
speeds respectively. We can get
8
<
:
T
o
¼ðT
r
þ T
mot1
r
mot1
Þ$r
final
w
mot1
¼ w
o
=
r
final
r
mot1
w
r
¼ w
o
=r
final
(7)
where r
final
, and r
mot1
are the gear ratios between driveline and
vehicle wheels, motor 1 and driveline, respectively. The planetary
gear set consists of a ring gear, a sun gear, and carrier [2,9], which
connects driveline, motor 2, and the engine respectively. Neglecting
inertia losses and friction, there are two basic equations for torque
and speed of the planetary gear set
T
e
¼ð1 þ 1=
r
Þ$T
mot2
¼ð1 þ
r
Þ$T
r
ð1 þ
r
Þ$w
e
¼
r
$w
mot2
þ w
r
(8)
where
r
is the ratio between sun gear and ring gear, w
mot2
, w
e
denote the speed of motor 2, engine, and T
mot2
and T
e
are their
torques. Based on Eqs. (6)e(8), we can calculate T
e
further
T
e
¼
T
o
T
mot1
1þ
r
¼
T
o
P
mot1
=
ð
r
final
w
o
Þ
1þ
r
¼
T
o
ðP
b
P
a
P
mot2
Þ$
h
mot1
=
ð
r
final
w
o
Þ
1þ
r
¼
T
o
ðP
b
P
a
T
mot2
w
mot2
=
h
mot2
Þ$
h
mot1
=
ð
r
final
w
o
Þ
1þ
r
¼
1
1þ
r
$
h
T
o
P
b
P
a
T
e
$
ð
ð1þ
r
Þ$w
e
r
final
w
o
Þ
h
mot2
ð
r
þ1Þ
$
h
mot1
=
r
final
w
o
i
¼
1
1þ
r
$
T
o
ðP
b
P
a
Þ$
h
mot1
r
final
w
o
þ
1
ð1þ
r
Þ
2
$
ð
ð1þ
r
Þ$w
e
r
final
w
o
Þ
r
final
w
o
$
h
mot1
h
mot2
$T
e
(9)
where
h
mot1
and
h
mot2
represent efficiencies of motor 1 and motor
2. Solving Eq. (9), we can get
T
e
¼
1
1þ
r
$
T
o
ðP
b
P
a
Þ$
h
mot1
r
final
w
o
1
1
ð1þ
r
Þ
2
$
ð
ð1þ
r
Þ$w
e
r
final
w
o
Þ
r
final
w
o
$
h
mot1
h
mot2
¼ gðT
o
; P
b
; w
o
; w
e
Þ (10)
From Eq. (10), T
e
can be determined by P
b
, T
o
, w
o
, and w
e
. P
b
can
be approximately calculated using battery open circuit voltage V
ocv
,
battery current I, and battery internal resistance R [8],
P
b
¼ V
ocv
I þ I
2
R (11)
Hence, according to Eqs. (10) and (11), Eq. (2) can be changed to
m
f
¼ f ðT
e
; w
e
Þ¼f
new
ðT
o
; w
o
; I; w
e
Þ (12)
Fig. 2. Idealized vehicle driveline power distribution.
Z. Chen et al. / Journal of Power Sources 248 (2014) 416e426418









