四元数值回声状态网络：3D与4D过程建模新方法
104 浏览量
更新于2024-08-29
收藏 1.24MB PDF 举报
"Quaternion-valued Echo State Networks for 3-D and 4-D process modeling in renewable energy and human-centered computing applications, utilizing quaternion nonlinear activation functions and augmented quaternion statistics for second-order optimality in widely linear models."
在神经网络和学习系统领域，四元数值回声状态网络（Quaternion-Valued Echo State Networks, QESNs）是一种新兴的技术，专门针对三维（3-D）和四维（4-D）过程的建模。这些过程可能出现在可再生能源，如3-D风力建模，以及人本计算中，如3-D惯性身体传感器数据处理。QESNs的提出得益于近期四元数非线性激活函数的发展，这些函数具有局部解析性质，满足非线性梯度下降训练算法的需求。
四元数是一种扩展复数的概念，可以更有效地处理多维数据，特别是对于3-D和4-D信号。传统的回声状态网络（Echo State Networks, ESNs）在处理一维或二维数据时表现出色，但QESNs的出现使得处理更高维度的数据成为可能。在QESNs中，回声状态网络的动态水库，通常由递归神经网络实现，能够充分利用四元数表示的特性。
为了使QESNs对各种四元数信号（无论是圆形还是非圆形）达到第二阶最优，论文引入了增强的四元数统计（augmented quaternion statistics）。这涉及到广泛线性QESNs的概念，其中标准的广泛线性模型被修改以适应动态水库的特性。这种方法允许全面利用数据中的第二阶信息，包括协方差和伪协方差，从而实现严谨的分析和更精确的建模。
通过这样的方法，QESNs不仅可以捕获信号的主要趋势，还能捕捉到信号的复杂结构和非线性关系，这对于理解和预测3-D和4-D过程至关重要。在可再生能源领域，例如风力预测，准确的三维模型可以帮助优化能源生产；而在人类中心计算中，四元数模型能够改进基于人体运动传感器数据的分析和应用。
QESNs结合了四元数数学的高效性和回声状态网络的强学习能力，为高维复杂系统的建模提供了一种创新且强大的工具。这种技术有望在未来的可再生能源预测、人体运动追踪以及其他依赖多维数据处理的应用中发挥重要作用。
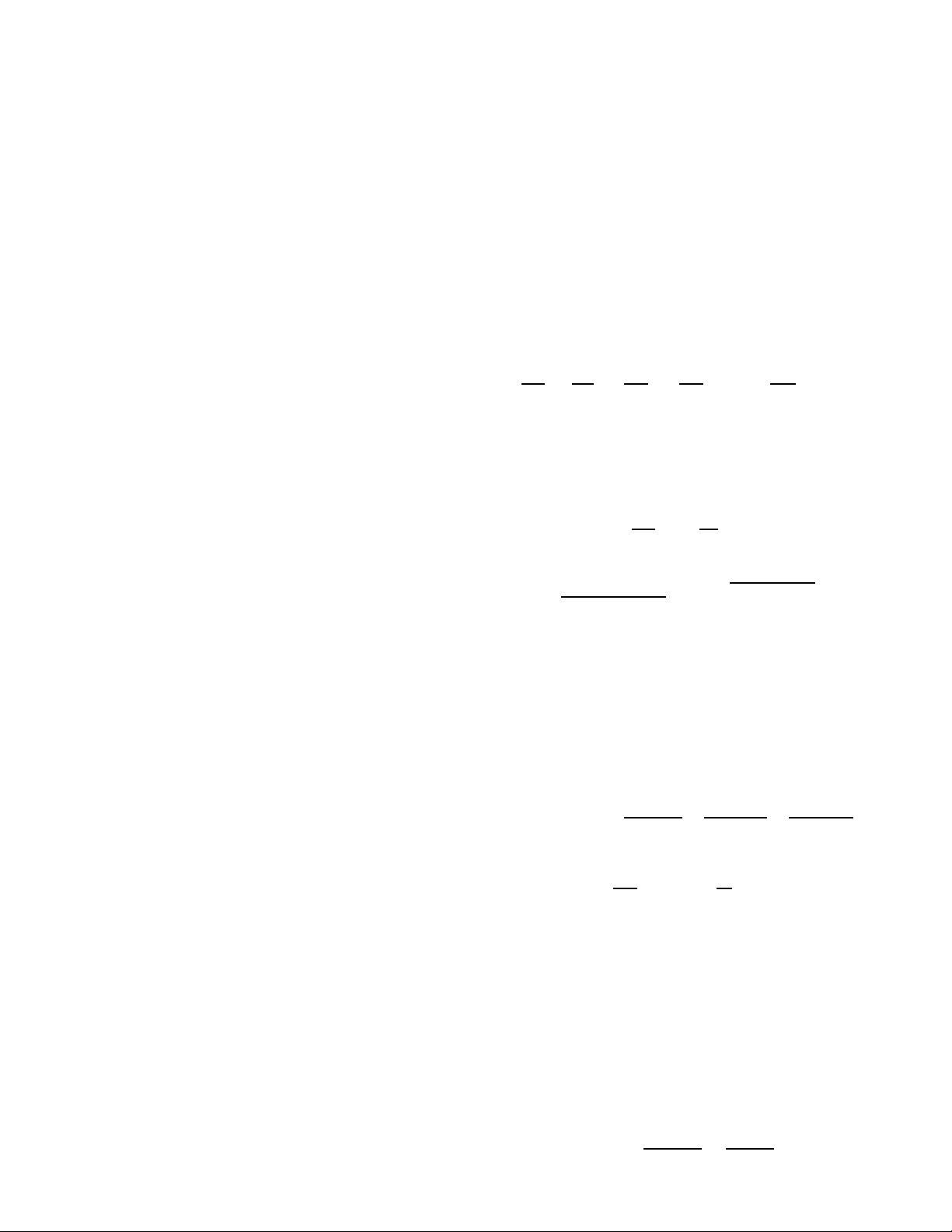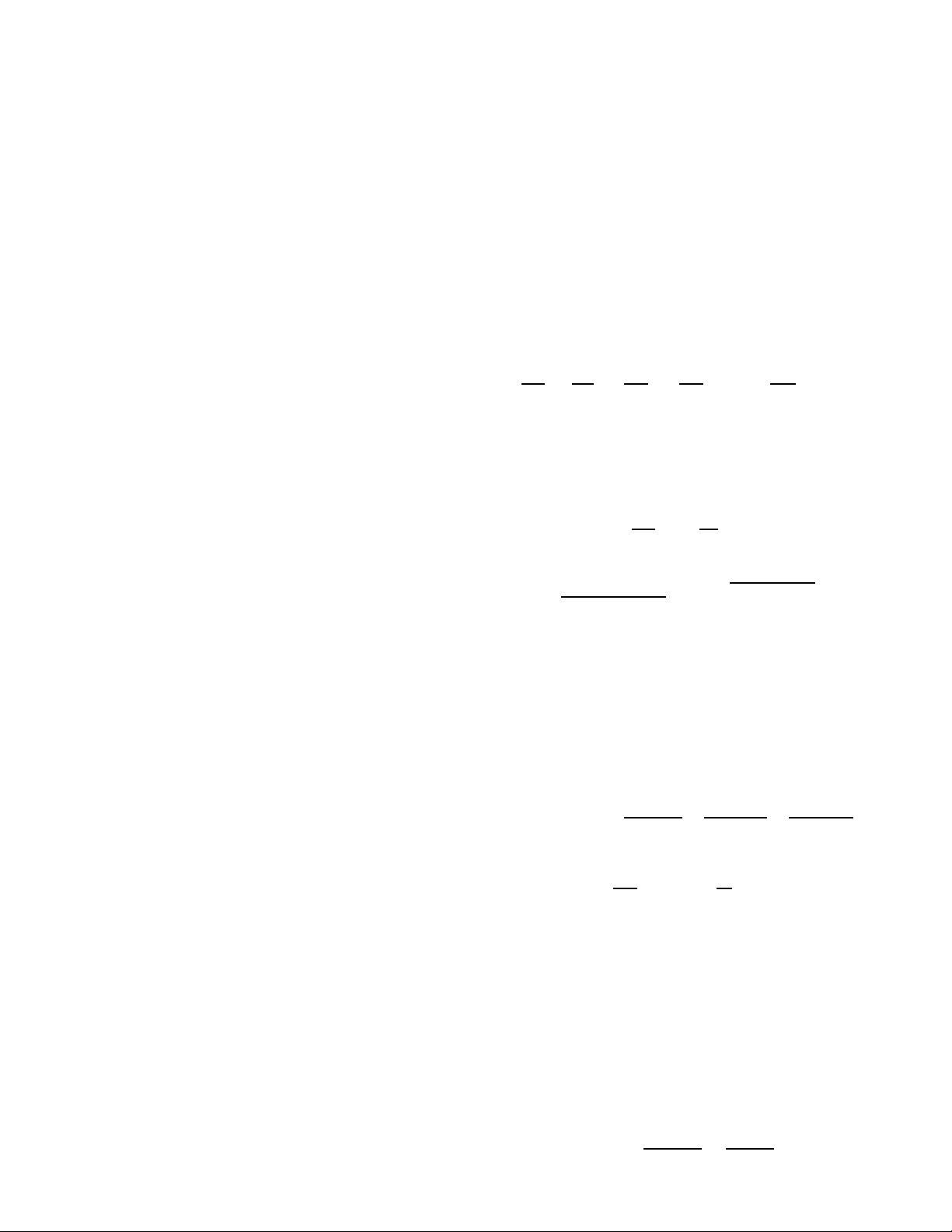
XIA et al.: QUATERNION-VALUED ECHO STATE NETWORKS 665
A. Augmented Quaternion Statistics
Unlike the real domain where complete second-order statis-
tics of a random vector q(k) are described by the covariance
matrix R = E[qq
T
], in the complex and quaternion domains,
the covariance matrix is sufficient to describe only second-
order circular (proper) signals, which have equal power in data
components. For general second-order noncircular (improper)
quaternion signals, where powers in the data components may
be different, for optimal second-order modeling, we also need
to employ complementary covariance matrices (pseudocovari-
ances). These complementary covariance matrices are termed
the ı-covariance P, j-covariance S and κ-covariance T,and
are given by [16], [29]–[32]
P = E[qq
ıH
], S = E[qq
jH
], T = E[qq
κT
].
Remark 1: Complete second-order characteristics of a
quaternion random vector q are then described by the aug-
mented covariance matrix R
a
of an augmented vector q
a
=
[q
T
, q
ıT
, q
jT
, q
κH
]
T
,givenby
R
a
= E[q
a
q
aH
]=
⎡
⎢
⎢
⎣
RPST
P
ı
R
ı
T
ı
S
ı
S
j
T
j
R
j
P
j
T
κ
S
κ
P
κ
R
κ
⎤
⎥
⎥
⎦
. (5)
Notice that for proper signals, the pseudocovariance matrices
P, S,andT vanish; a signal that obeys this structure has a
probability distribution that is rotation invariant with respect
to all the six possible pairs of axes [16], [29]–[32]. However,
in most of the real-world applications, probability density
functions are rotation dependent, and hence require the use
of the augmented quaternion statistics.
B. Quaternion Widely Linear Model
To exploit the complete second-order statistics of
quaternion-valued signals in linear mean square error (MSE)
estimation, we first consider a quaternion-valued MSE
estimator given by
ˆy = E[y|q]
where ˆy is the estimated process, q the observed variable, and
E[·] the statistical expectation operator. For zero-mean jointly
normal q and y, the strictly linear estimation solution, similar
to those in R and C,isgivenby
ˆy = w
T
q
where w and q are, respectively, the coefficient and regressor
vector. Observe, however, that for all the components {y
r
, y
ı
,
y
j
, y
κ
}, we have
ˆy
η
= E[y
η
|q
r
, q
ı
, q
j
, q
κ
],η∈{r, ı,j,κ}
so that using the involutions in (1), we can express each
element of a quaternion variable as in (2). This gives, for
instance, for the real component of a quaternion variable
q
r
= (q + q
ı
+ q
j
+ q
κ
)/4, leading to the general expression
for all the components
ˆy
η
= E[y
η
|q, q
ı
, q
j
, q
κ
], and ˆy = E[y|q, q
ı
, q
j
, q
κ
].
In other words, to capture the full second-order information
available, we should use the original quaternion and its invo-
lutions, allowing us to arrive at the widely linear model [16],
[29], [30]
y = w
aT
q
a
= a
T
q + b
T
q
ı
+ c
T
q
j
+ d
T
q
κ
(6)
where w
a
=[a
T
, b
T
, c
T
, d
T
]
T
is the augmented weight vector.
IV. N
ONLINEAR ACTIVATION FUNCTIONS IN H
One of the difficulties in the design of hypercomplex RNNs
lies in the lack of analytic nonlinear activation functions, as
the CRF conditions for analyticity in H are very stringent [17].
For instance, a CRF differentiable quaternion function f (q)
should satisfy
∂ f
∂q
r
+ ı
∂ f
∂q
ı
+ j
∂ f
∂q
j
+ κ
∂ f
∂q
κ
= 0 ⇔
∂ f
∂q
∗
= 0. (7)
Only linear quaternion functions and constants fulfill these
conditions, yet nonlinear adaptive filtering in H requires dif-
ferentiable nonlinear functions. To circumvent the analyticity
problem, recent work in [24] adopted the LAC [23], based on
a complex-valued representation of a quaternion, to give
∂ f
∂q
r
=−ζ
∂ f
∂α
(8)
where ζ and α are, respectively, given by
ζ =
ıq
ı
+ j q
j
+ κq
κ
α
,α=
q
2
ı
+ q
2
j
+ q
2
κ
. (9)
In this way, an imaginary unit ζ comprises the vector part
of quaternions. Although the LAC only guarantees first-order
differentiability at the current operating point, this is a perfect
match for quaternion-valued gradient algorithms, which only
require gradient evaluation at a point.
Proposition 1: The quaternion exponential e
q
=
e
q
r
+ıq
ı
+jq
j
+κq
κ
satisfies the LAC in (8).
Proof: e
q
can be expanded using the Euler formula as
e
q
= e
q
r
(cos(α) + ζ sin(α))
= e
q
r
cos(α) +
ıq
ı
sin(α)
α
+
jq
j
sin(α)
α
+
κq
κ
sin(α)
α
where ζ and α are defined in (9), to give
∂e
q
∂q
r
= e
q
=−ζ
e
q
α
. (10)
Remark 2: Notice that the quaternion exponential e
−q
=
e
−(q
r
+ ıq
ı
+ jq
j
+ κq
κ
)
also satisfies the LAC in (8). This is
straightforward to show using the same approach as in
Proposition 1.
Remark 3: Quaternion transcendental nonlinear func-
tions, constructed on the basis of quaternion exponentials
e
q
and e
−q
, are a generic extension of those in R and C,
and also satisfy the LAC.
For a detailed proof of Remark 3, we refer to [24].
In this paper, we employ a fully quaternion tanh(q) function
to design the QESNs, defined as
tanh(q) =
e
q
− e
−q
e
q
+ e
−q
=
e
2q
− 1
e
2q
+ 1
(11)
剩余10页未读，继续阅读
568 浏览量
2021-08-19 上传
106 浏览量
2021-09-27 上传
383 浏览量
131 浏览量
2022-01-06 上传
2022-07-13 上传
2021-02-21 上传
weixin_38569515
- 粉丝: 2
我的内容管理
展开
最新资源
- RabbitMQ订阅模式压力测试与性能分析
- 配套网页设计的图片资源压缩包
- SpringBoot集成Mybatis与Quartz的高级技术应用
- Matlab编辑器文件自动恢复功能实现
- Rust宏：const_random! 在编译时生成随机常量
- 使用pandas实现Excel数据操作与分析教程
- OpenCv2在C++中的应用与实践指南
- UCB算法与程序设计课程主要内容概述
- 易语言JSON模块修改版特性解析及使用
- Vivado环境下ZedBoard上实现PL流水灯教程
- TeXPower开源软件：动态LaTeX在线演示解决方案
- 全面解析开发套件：CLI与Angular SDK
- MySQL国家行政代码包，数据库开发者的福音
- 笔记本端一键开启WiFi热点共享技巧
- Matlab环境配置：启动脚本与日记功能
- 火星车导航优化与通信自检技术研究
