特殊马氏链首达问题：对称性与计算机模拟

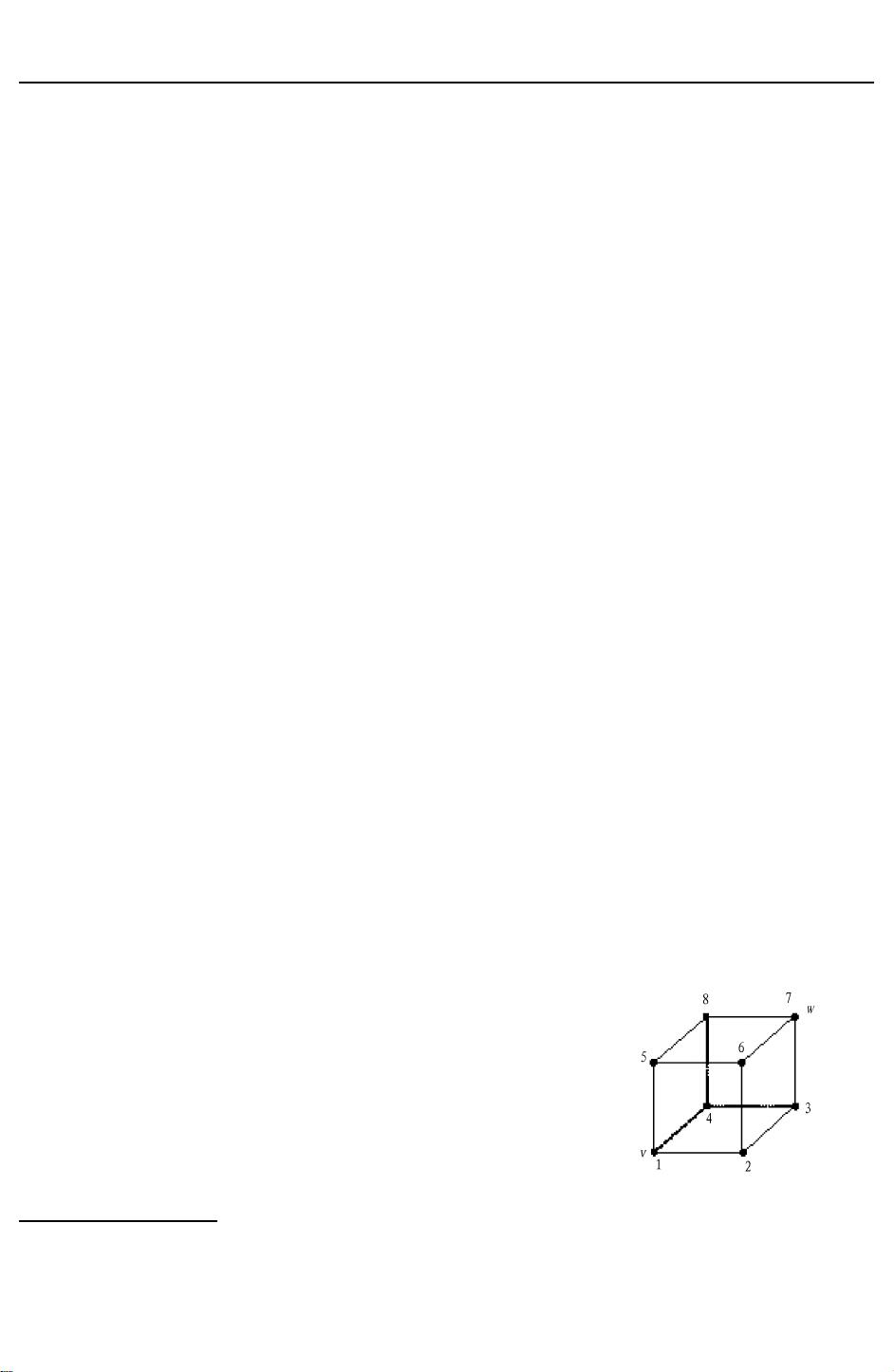
本文主要探讨了一类特殊类型的马尔可夫链——立方体和锥体上的随机游走，其中游走者在这些几何结构上等概率地进行有逗留和无逗留的移动。研究的核心内容包括该马氏链的平稳分布、平均回返时间和首次回返时间的计算。作者通过细致的理论分析，利用状态空间的对称性，得出了对于特定状态a，何时能先达到状态b的概率，这是对传统马尔可夫链理论的创新应用。 在立方体模型中，质点从一个顶点（如v）出发，每一步可能停留在当前位置或者移动到任意一个相邻顶点，概率各为1/4。作者定义了自状态i到状态j在n步后的概率Pij(n)，这对于理解整个过程的动态至关重要。 而在n面锥体的随机游走模型中，作者考虑了两种情况：一是质点在n边形平面内随机移动，不包括自身；二是每个状态均等概率地移动到相邻点，包括自身。这种复杂性增加了问题的挑战性和研究的深度。 文章的预备知识部分介绍了马尔可夫链的基本概念，即自初始状态i出发经过n步到达状态j的概率Pij(n)的定义。对于不可达的状态，文章也做了相应的处理，强调了链的连通性。 本文不仅深入探讨了理论分析，还通过数值模拟的方法来验证所得结论，这在现代计算机科学中是常见的方法，可以帮助研究人员更好地理解和应用马尔可夫链的原理。通过这种结合理论与实践的研究，作者揭示了这类特殊马氏链的独特性质，对于理解和优化随机过程在实际问题中的应用具有重要意义。 这篇论文提供了对一类特殊马尔可夫链在立方体和锥体上的随机游走的深入洞察，展示了如何利用状态空间的对称性进行问题求解，并通过计算机模拟验证理论成果，对于马尔可夫链理论的发展和实际应用领域都具有较高的价值。