微电子电路与器件概览

4星 · 超过85%的资源 | 下载需积分: 49 | PDF格式 | 44.41MB | 更新于2024-07-28 | 62 浏览量 | 举报

2 收藏

"Microelectronic Circuits, Sedra, Smith" "Microelectronic Circuits" 是一本深入探讨微电子电路的经典教材，由Adel S. Sedra和Paul C. Smith共同编写。该书是牛津电气与计算机工程系列的一部分，涵盖了微电子领域的广泛主题，适合于电气工程和计算机科学的学生以及专业人士学习。本书的核心内容可能包括以下几个方面： 1. **微电子基础**：讲解半导体物理学的基础，包括晶体管（BJT和MOSFET）的工作原理、特性曲线以及它们在放大和开关应用中的作用。 2. **模拟电路设计**：涵盖基本的放大器设计，如共射极、共集电极和共基极放大器，以及运算放大器的应用，如电压跟随器、比较器、滤波器等。 3. **数字逻辑**：介绍基本的逻辑门电路、组合逻辑和时序逻辑电路，包括触发器、计数器和存储器的设计。 4. **集成电路**：讨论集成电路制造过程，包括CMOS工艺，以及如何设计和分析混合信号集成电路。 5. **线性系统理论**：涵盖线性电路的分析方法，如节点电压法、环路电流法和超定系统的解法。 6. **信号与系统**：阐述信号的基本性质，如傅里叶变换，以及系统的时域和频域分析。 7. **概率方法**：在信号和系统分析中引入概率论，用于处理随机信号和噪声。 8. **半导体设备理解**：深入探讨半导体材料的物理特性和半导体器件的性能。 9. **电力电子与变压器**：介绍电动机、发电机和变压器的工作原理及其在电力系统中的应用。 10. **电子测量与测试**：讨论混合信号系统的测试和测量技术，包括示波器、逻辑分析仪等仪器的使用。 11. **电路分析**：提供电路分析的基本方法，如欧姆定律、基尔霍夫定律和网络定理。 12. **数字信号处理**：涉及离散时间信号的处理，包括采样理论、数字滤波器和数字信号处理器。 13. **微处理器系统设计**：讲解微处理器的架构、指令集和微程序设计。通过这本书，读者可以全面了解微电子学的各个方面，从基础概念到高级设计，从而具备设计和分析现代电子系统的能力。

CHAPTER

Introduction

Electronics

CHAPTER

Operational Amplifiers

CHAPTER

Diodes

139

CHAPTER

MOS Field-Effect Transistors (MOSFETs)

235

CHAPTER

Bipolar Junction Transistors (BJTs)

377

INTRODUCTION

Part

Devices

and

Basic Circuits, includes

the

most fundamental

and

essential topics

for

the

study

electronic circuits.

At the

same time,

constitutes

complete pack-

age

for a

first course

on the

subject.

Besides silicon diodes

and

transistors,

the

basic electronic devices,

the op amp is

studied

Part

Although

not an

electronic device

in the

most fundamental sense,

the

op amp is

commercially available

as an

integrated circuit

(IC)

package

and has

well-defined terminal characteristics. Thus, despite

the

fact that

the op

amp's internal

circuit

complex, typically incorporating

20 or

more transistors,

its

almost-ideal ter-

minal behavior makes

possible

treat

the op amp as a

circuit element

and to use it

the

design

powerful circuits,

as we do in

Chapter

without

any

knowledge

its internal construction.

should mention, however, that

the

study

of op

amps

can

be delayed

to a

later point,

and

Chapter

2 can be

skipped with

loss

continuity.

The most basic silicon device

is the

diode.

addition

learning about diodes

and

sample

their applications, Chapter

also introduces

the

general topic

device modeling

for the

purpose

circuit analysis

and

design. Also, Section

3.7

pro-

vides

substantial introduction

to the

physical operation

semiconductor devices.

This subject

then continued

Section

4.1 for the

MOSFET

and in

Section

5.1 for

the B

JT.

Taken together, these three sections provide

physical background sufficient

for

the

study

electronic circuits

at the

level presented

this book.

The heart

this book,

and of any

electronics course,

is the

study

the

two

transis-

tor types

in use

today:

the MOS

field-effect transistor (MOSFET)

Chapter

4 and the

bipolar junction transistor (BJT)

Chapter

These

two

chapters have been written

to be

completely independent

of one

another

and

thus

can be

studied

either desired order.

Furthermore,

the two

chapters have

the

same structure, making

easier

and

faster

study

the

second device,

well

as to

draw comparisons between

the two

device types.

Chapter

provides both

introduction

to the

study

electronics

and a

number

of important concepts

for the

study

amplifiers (Sections

1.4-1.6)

and of

digital cir-

cuits (Section

1.7).

Each

of the

five chapters concludes with

section

on the use of

SPICE simula-

tion

circuit analysis

and

design.

particular importance here

are the

device mod-

els employed

SPICE. Finally, note that

as in

most

of the

chapters

this book,

the

must-know material

placed near

the

beginning

of a

chapter while

the

good-to-know

topics

are

placed

in the

latter part

of the

chapter. Some

this latter material

can

therefore

skipped

in a

first course

and

covered

at a

later time, when needed.

üüm

HÜLL

HV.~

WÊÊÊm^

WÈÈÈÊKÊÈ

-ic~

ïlliiw

C »Je

-• CHAPTER

INTRODUCTION

ELECTRONICS

In addition

motivating

the

study

electronics, this chapter serves

as a

bridge between

the study

linear circuits

and

that

of the

subject

this book:

the

design

and

analysis

electronic circuits.

1.1 SIGNALS

Signals contain information about

variety

things

and

activities

in our

physical world.

Examples abound: Information about

the

weather

contained

signals that represent

the

air temperature, pressure, wind speed, etc.

The

voice

of a

radio announcer reading

the

news

into

microphone provides

acoustic signal that contains information about world affairs.

To monitor

the

status

of a

nuclear reactor, instruments

are

used

measure

multitude

relevant parameters, each instrument producing

signal.

To extract required information from

a set of

signals,

the

observer

(be it a

human

or a

machine) invariably needs

process

the

signals

some predetermined manner. This signal

processing

usually most conveniently performed

electronic systems.

For

this

to be

possible, however,

the

signal must first

converted into

electric signal, that

is, a

voltage

current. This process

accomplished

devices known

transducers.

variety

transducers exist, each suitable

for one of

the various forms

physical signals.

For

instance,

the sound waves generated

by a

human

can be

converted into electric signals using

micro-

phone, which

is in

effect

pressure transducer.

It is not our

purpose here

study transduc-

ers;

rather,

shall assume that

the

signals

interest already exist

in the

electrical domain

and represent them

by one of

the two equivalent forms shown

Fig. 1.1.

Fig.

1.1(a)

the

sig-

nal

represented

by a

voltage source

(t)

having

source resistance

. In the

alternate

representation

Fig.

1.1(b)

the

signal

represented

by a

current source

(t)

having

source

resistance

Although

the two

representations

are

equivalent, that

Fig.

1.1(a)

(known

the Thevenin form)

preferred when

low.

The

representation

Fig.

1.1(b)

(known

the Norton form)

preferred when

high.

The

reader will come

appreciate this point

later

this chapter when

study

the

different types

amplifiers.

For the

time being,

it is

important

to be

familiar with Thevenin's

and

Norton's theorems

(for a

brief review,

see

Appendix

D) and to

note that

for the two

representations

Fig.

1.1 to be

equivalent, their

parameters

are

»,(/)

R,i,(t)

From

the

discussion above,

should

apparent that

signal

is a

time-varying quantity

that

can be

represented

by a

graph such

that shown

in Fig. 1.2. In

fact,

the

information

content

of the

signal

represented

by the

changes

in its

magnitude

time progresses; that

is,

the

information

contained

in the

"wiggles"

in the

signal waveform.

general, such

waveforms

are

difficult

characterize mathematically.

other words,

it is not

easy

describe succinctly

arbitrary-looking waveform such

that

Fig.

1.2. Of

course, such

° FIGURE

1.1 Two alternative representa-

tions of

signal source:

(a)

the Thevenin

(

)

(b)

form, and (b) the Norton form.

1.2 FREQUENCY SPECTRUM

SIGNALS

^.(0 A

Time,

FIGURE

1.2

An arbitrary voltage signal

(t).

description

is of

great importance

for the

purpose

designing appropriate signal-processing

circuits that perform desired functions

on the

given signal.

EXERCISES

sMMIoPithe

signal-source representations shown

Figs.

1.1(a)

and

1.1(b). what

arc the

open-circuit

out-

put voltages that would

observed?

If, for

each,

the

output terminals

are

short-circuited (i.e.. wired

together), what

current

would

flow? For

the representations to be equivalent,

what must

the relationship

between

, and R/>

Ans.

For (a), v

«,(/);

for (b), v

. =

R,ift):

for (a), i

(t)/R>;

for (b), i

. =

i,(t):

for

equivalency,

(t) =

(t)

1.2 A

signal source

has an

open-circuit voltage

of 10 mV and a

short-circuit current

of 10

/iA. What

is the

source resistance?

Ans. 1

k*2

1.2 FREQUENCY SPECTRUM

SIGNALS

An extremely useful characterization

of a

signal,

and for

that matter

of any

arbitrary func-

tion

time,

is in

terms

of its

frequency spectrum. Such

description

signals

obtained

through

the

mathematical tools

Fourier series

and

Fourier transform.

We are not

interested

this point

in the

details

these transformations; suffice

it to say

that they pro-

vide

the

means

for

representing

voltage signal

(t) or a

current signal

(t) as the sum of

sine-wave signals

different frequencies

and

amplitudes. This makes

the

sine wave

very

important signal

in the

analysis, design,

and

testing

electronic circuits. Therefore,

shall briefly review

the

properties

the sinusoid.

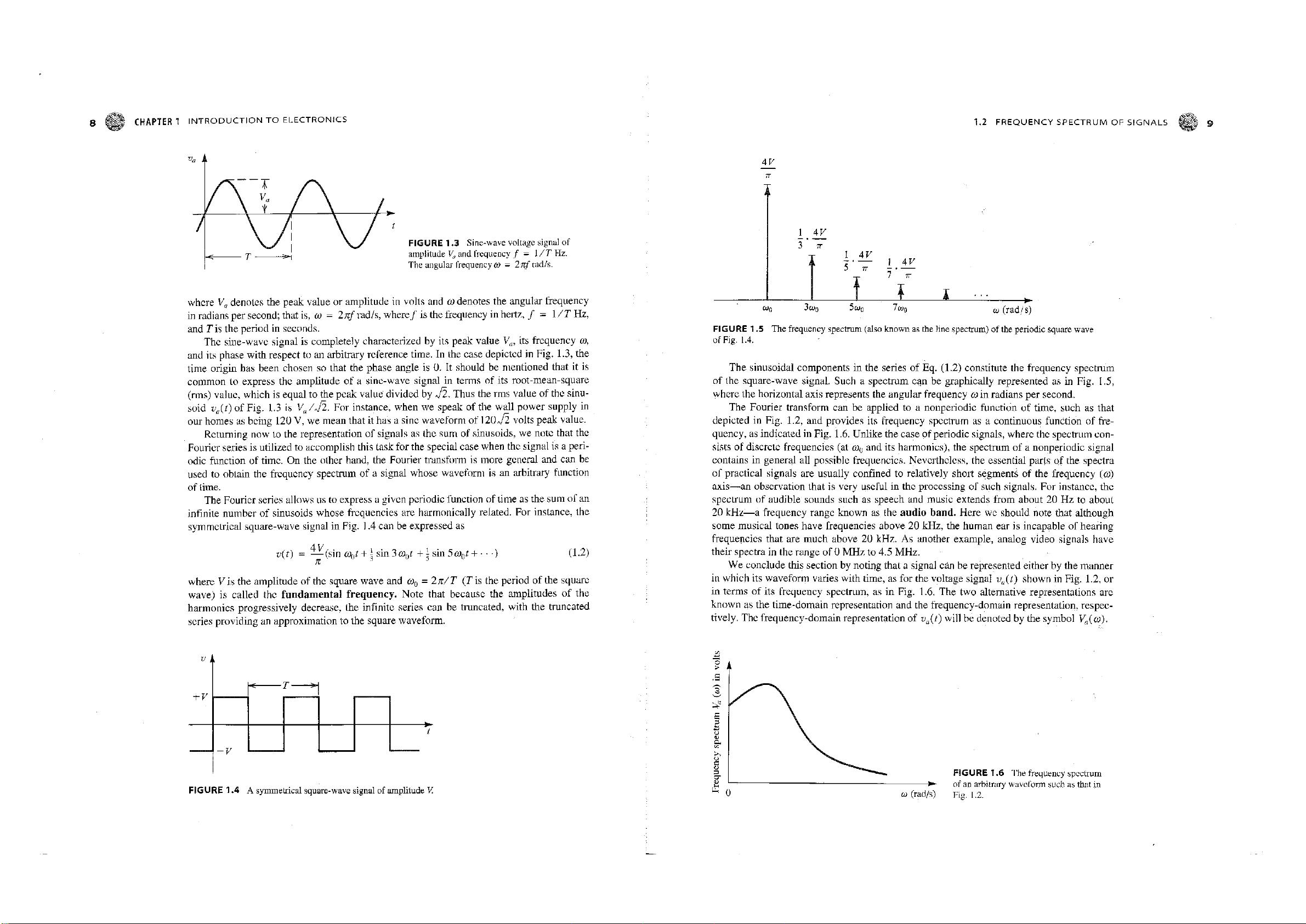
Figure

1.3

shows

sine-wave voltage signal v

(t),

(t)

sin

cot . (1.1)

The reader who has

not yet

studied these topics should not be alarmed.

detailed application of this

material will be made until Chapter 6. Nevertheless,

general understanding

Section

1.2

should

very helpful when studying early parts

this book.

CHAPTER

INTRODUCTION

ELECTRONICS

FIGURE

1.3 Sine-wave voltage signal of

amplitude V

and frequency / = 1/7* Hz.

The angular frequency

= 2^frad/s.

where V

denotes the peak value or amplitude in volts and co denotes the angular frequency

in radians per second; that is, co - 2nf rad/s, where/ is the frequency in hertz, / = l/T Hz,

and T is the period in seconds.

The sine-wave signal is completely characterized by its peak value V

, its frequency co,

and its phase with respect to an arbitrary reference time. In the case depicted in Fig. 1.3, the

time origin has been chosen so that the phase angle is 0. It should be mentioned that it is

common to express the amplitude of a sine-wave signal in terms of its root-mean-square

(rms) value, which is equal to the peak value divided by J2. Thus the rms value of the sinu-

soid v

{t) of Fig. 1.3 is

/j2.

For instance, when we speak of the wall power supply in

our homes as being 120 V, we mean that it has a sine waveform of 120 Jl volts peak value.

Returning now to the representation of signals as the sum of sinusoids, we note that the

Fourier series is utilized to accomplish this task for the special case when the signal is a peri-

odic function of time. On the other hand, the Fourier transform is more general and can be

used to obtain the frequency spectrum of a signal whose waveform is an arbitrary function

of time.

The Fourier series allows us to express a given periodic function of time as the sum of an

infinite number of sinusoids whose frequencies are harmonically related. For instance, the

symmetrical square-wave signal in Fig. 1.4 can be expressed as

v(t) = —(sin co

t + \ sin 3co

t + \ sin 5co

t + • • •)

(1.2)

where V is the amplitude of the square wave and co

= 2n/T (T is the period of the square

wave) is called the fundamental frequency. Note that because the amplitudes of the

harmonics progressively decrease, the infinite series can be truncated, with the truncated

series providing an approximation to the square waveform.

+ V

-T—SI-

FIGURE

1.4 A symmetrical square-wave signal of amplitude V.

1.2

FREQUENCY SPECTRUM

SIGNALS

3 ' TT

5 " TT

I iE

7 ' 7T

T *

5a)

7cu

(u (rad/s)

FIGURE

1.5 The frequency spectrum (also known as the line spectrum) of the periodic square wave

of Fig. 1.4.

The sinusoidal components in the series of Eq. (1.2) constitute the frequency spectrum

of the square-wave signal. Such a spectrum can be graphically represented as in Fig. 1.5,

where the horizontal axis represents the angular frequency

in radians per second.

The Fourier transform can be applied to a nonperiodic function of time, such as that

depicted in Fig. 1.2, and provides its frequency spectrum as a continuous function of fre-

quency, as indicated in Fig. 1.6. Unlike the case of periodic signals, where the spectrum con-

sists of discrete frequencies (at co

and its harmonics), the spectrum of a nonperiodic signal

contains in general all possible frequencies. Nevertheless, the essential parts of the spectra

of practical signals are usually confined to relatively short segments of the frequency (co)

axis—an observation that is very useful in the processing of such signals. For instance, the

spectrum of audible sounds such as speech and music extends from about 20 Hz to about

20 kHz—a frequency range known as the audio band. Here we should note that although

some musical tones have frequencies above 20 kHz, the human ear is incapable of hearing

frequencies that are much above 20 kHz. As another example, analog video signals have

their spectra in the range of 0 MHz to 4.5 MHz.

We conclude this section by noting that a signal can be represented either by the manner

in which its waveform varies with time, as for the voltage signal v

(t) shown in Fig. 1.2, or

in terms of its frequency spectrum, as in Fig. 1.6. The two alternative representations are

known as the time-domain representation and the frequency-domain representation, respec-

tively. The frequency-domain representation of v

(t) will be denoted by the symbol V

( co).

co (rad/s)

FIGURE

1.6 The frequency spectrum

of an arbitrary waveform such as that in

Fig. 1.2.

O ylSi CHAPTER 1 INTRODUCTION TO ELECTRONICS

1.3

Find the frequencies/and to of a sine-wave signal with a period of

ms.

Ans.

/ ^ 1000 H/:

- In x 10

rad/s

1.4

What is the

period

T of

sine

waveforms characterized by

frequencies

of (a):f = 60 Hz? (b)/= IQ~'

}

Hz?

(c)/= 1 MHz? \}-]

Ans.

16.7 ms; 1000 s; 1 £is

TiS

; The UHF (Ultra High Frequency) television broadcast band begins

with

channel 14 and extends from

•^.mWJO

MHz lo 806 MHz. If 6 MHz is allocated for each channel, how manytchannels can this band

accommodate?

ssAns.

56; channels 14 to 69

1.6

When the square-wave signal of Fig. 1.4, whose Fourier series is given in Eq. (1.2), is applied to a resistor,

the total power dissipated may be calculated directly using the relationship

JP]

= 1/T

\l{v

/R)dl

or indirectly by summing the contribution of each of the harmonic components, that is, P = P,+

+ P

+ • • •, which may be found directly from rms values. Verify that the two approaches are equiv-

alent.

What

iVacumi of

(he

energy of a square wave is in its fundamental? In its first five harmonics'.' In

its first seven? First nine? In what number of harmonics is 90% of the energy? (Note that in counting

harmonies, the fundamental at co

is the first, the one at 2ft>„ is the second, etc.)

Ans. 0.81;

0.93; 0.95; 0.96; 3

1.3 ANALOG AND DIGITAL SIGNALS

The voltage signal depicted in Fig. 1.2 is called an analog signal. The name derives from

the fact that such a signal is analogous to the physical signal that it represents. The magni-

tude of an analog signal can take on any value; that is, the amplitude of an analog signal

exhibits a continuous variation over its range of activity. The vast majority of signals in the

world around us are analog. Electronic circuits that process such signals are known as

analog circuits. A variety of analog circuits will be studied in this book.

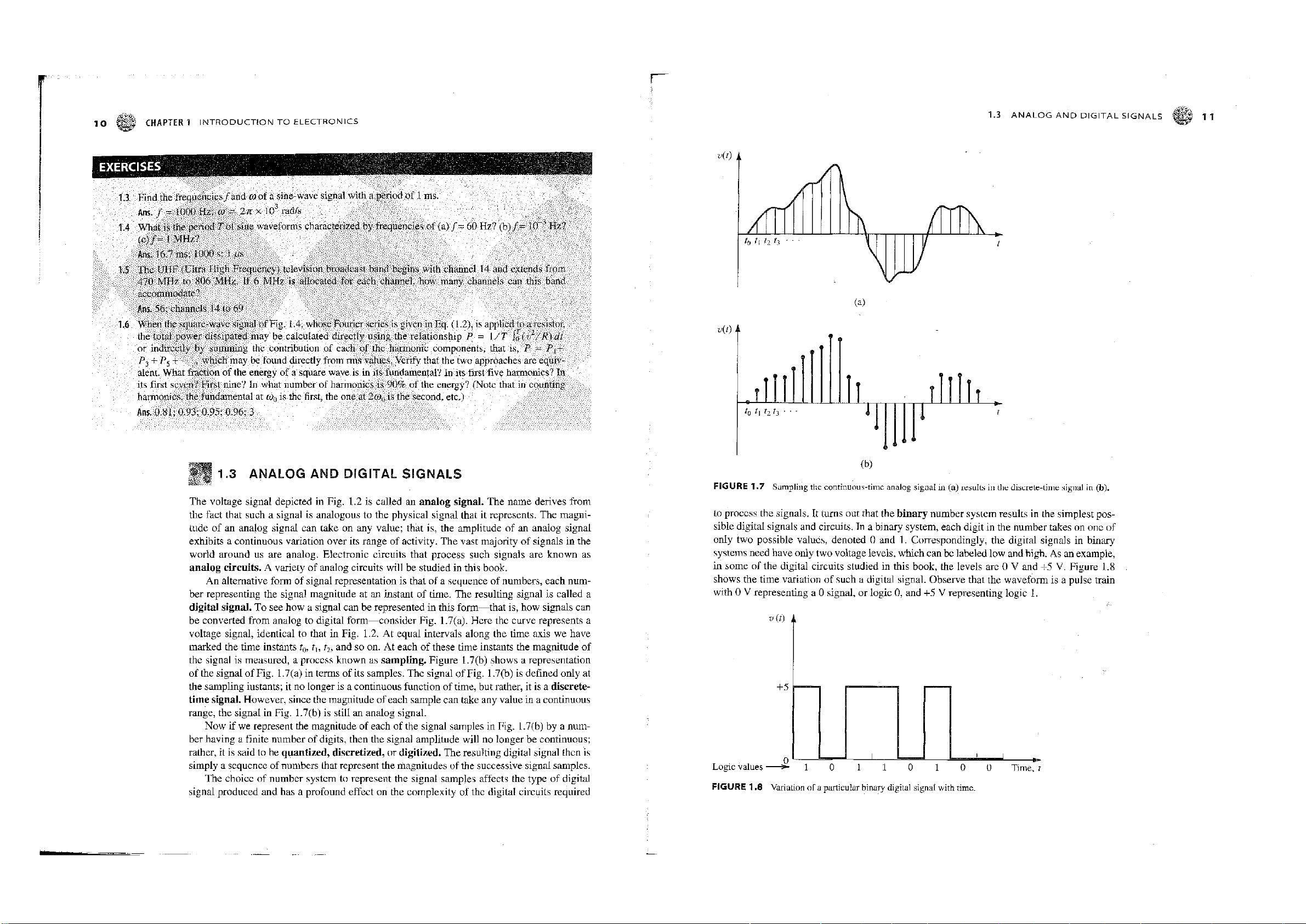
An alternative form of signal representation is that of a sequence of numbers, each num-

ber representing the signal magnitude at an instant of time. The resulting signal is called a

digital signal. To see how a signal can be represented in this form—that is, how signals can

be converted from analog to digital form—consider Fig.

1.7(a).

Here the curve represents a

voltage signal, identical to that in Fig. 1.2. At equal intervals along the time axis we have

marked the time instants t

, t

, and so on. At each of these time instants the magnitude of

the signal is measured, a process known as sampling. Figure

1.7(b)

shows a representation

of the signal of Fig.

1.7(a)

in terms of its samples. The signal of Fig.

1.7(b)

is defined only at

the sampling instants; it no longer is a continuous function of time, but rather, it is a discrete-

time signal. However, since the magnitude of each sample can take any value in a continuous

range,

the signal in Fig.

1.7(b)

is still an analog signal.

Now if we represent the magnitude of each of the signal samples in Fig.

1.7(b)

by a num-

ber having a finite number of digits, then the signal amplitude will no longer be continuous;

rather, it is said to be quantized, discretized, or digitized. The resulting digital signal then is

simply a sequence of numbers that represent the magnitudes of the successive signal samples.

The choice of number system to represent the signal samples affects the type of digital

signal produced and has a profound effect on the complexity of the digital circuits required

1.3 ANALOG AND DIGITAL SIGNALS I 11

v(t) k

h h h h • ' ' X

(a)

v(i)

,r!N

lllllt

h h h h ' ' ' 1 1

(b)

FIGURE

1.7 Sampling the continuous-time analog signal in

(a)

results in the discrete-time signal in (b).

to process the signals. It turns out that the binary number system results in the simplest pos-

sible digital signals and circuits. In a binary system, each digit in the number takes on one of

only two possible values, denoted 0 and 1. Correspondingly, the digital signals in binary

systems need have only two voltage levels, which can be labeled low and high. As an example,

in some of the digital circuits studied in this book, the levels are 0 V and +5 V. Figure 1.8

shows the time variation of such a digital signal. Observe that the waveform is a pulse train

with 0 V representing a 0 signal, or logic 0, and +5 V representing logic 1.

v(t) A

Logic values 5» 10 110 10 0 Time, t

FIGURE

1.8 Variation of a particular binary digital signal with time.

剩余695页未读，继续阅读

aaronaaronliang

粉丝: 0
资源: 5

微电子电路与器件概览

最新资源