小波分析入门：选择小波基函数的关键

"这篇文章主要介绍了小波分析的基本概念和应用，适合初学者入门。小波分析是一种强大的信号处理工具，可以进行局部分析，并在多种领域有广泛应用。文中提到了几种常见小波基函数，包括Haar、Daubechies、Morlet、Meyer、Symlet、Coiflet和Biorthogonal小波。此外，还讨论了小波系数的选择、尺度大小的影响以及小波分解层数与尺度的关系。" 小波分析是20世纪末发展起来的一种数学分析方法，它结合了傅立叶变换在频域分析的优点和时域分析的局限性，通过一种称为小波基的函数族来描述信号的时间-频率特性。这种分析方式允许我们同时查看信号在不同时间尺度上的局部特性，这对于检测信号中的瞬态变化或非平稳现象尤其有用。 小波基函数的选择对分析结果有很大影响。常见的小波函数如Haar小波因其简单的结构而在计算上较为简便；Daubechies小波（dbN）具有N个零点，能够更好地捕捉信号的细节；Morlet小波结合了复指数函数和高斯函数，适用于信号表示和特征提取；墨西哥帽小波（也即Morlet小波的一个特例）在系统识别中有良好表现；Symlet小波是对Daubechies小波的对称性改进；Coiflet小波提供更高的近似能力；而Biorthogonal小波则在正交性和重构质量之间取得平衡。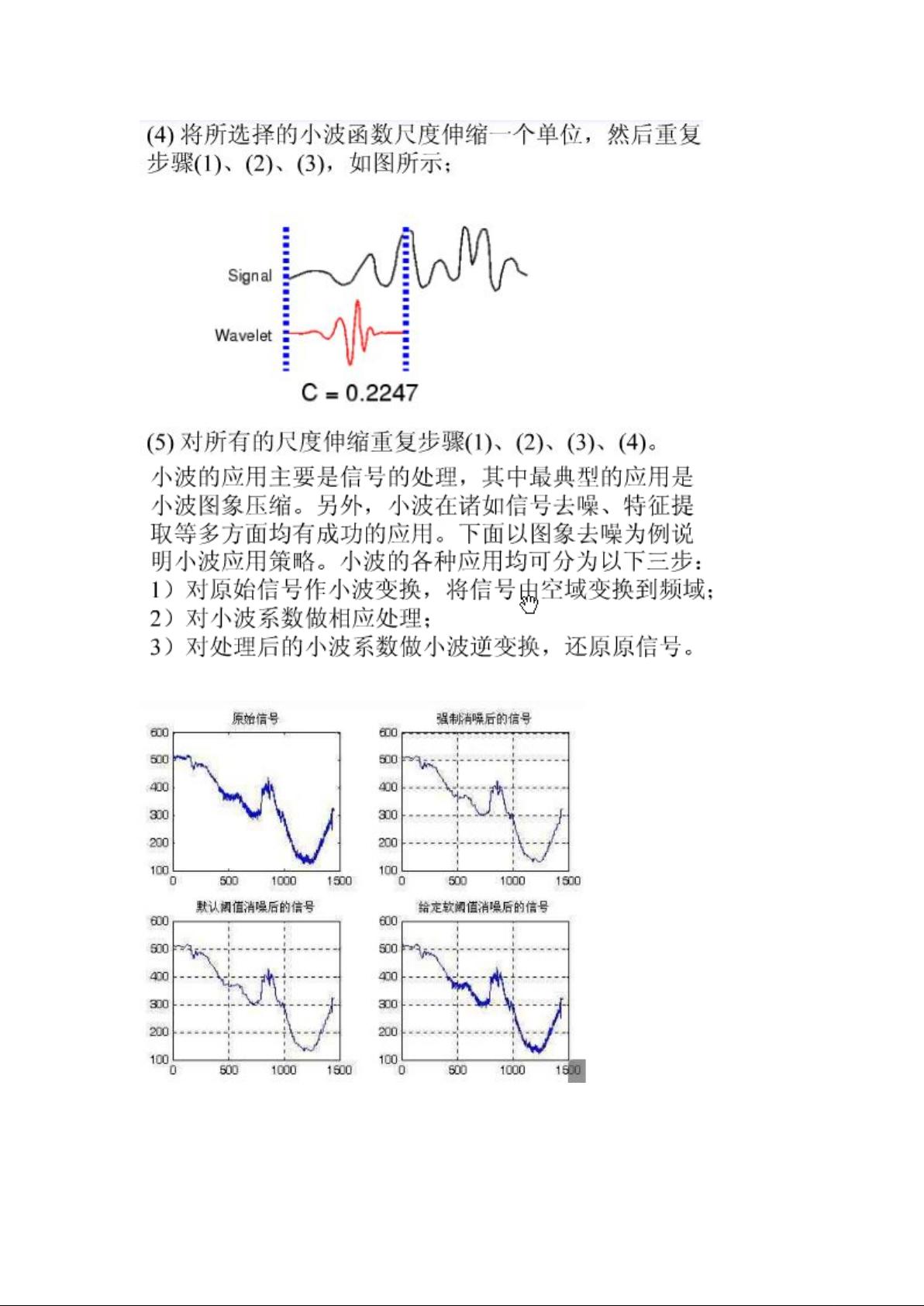 小波变换的小波系数可以帮助我们判断所选小波基函数与信号的匹配程度。较大的系数表示小波与信号波形相似度高，而较小的系数则表明匹配度低。尺度的选择取决于我们对信号分析的目标，大尺度通常用于捕获信号的整体趋势，小尺度则用于揭示细节信息。 多尺度分析是小波变换的核心概念。在连续小波变换（CWT）中，尺度决定了分析的分辨率，从小到大逐步变化，可以揭示信号在不同分辨率下的特征。例如，`wavedec`函数中的N参数代表分解层数，每一层对应一个不同的尺度，分解层数越多，分析的精细度越高。而`W=CWT(X,[2:2:128],'wname','plot')`中的尺度范围是从2到128，以2为步长，这表示在连续的尺度上进行变换。 多尺度的理解可以用空间分割的概念来阐述：初始空间（如0-pi）在每次分解后会被划分为高频和低频两部分，形成新的子空间。这样的分解过程不断进行，直到达到所需的分解层数或满足特定条件，这样就可以深入地剖析信号的多层次结构。 小波分析提供了一种灵活且强大的工具，适用于信号处理、图像分析、故障诊断、材料检测等多个领域，其理论和应用都值得深入研究。对于初学者来说，了解小波基函数、尺度选择和多尺度分析的基本原理，是掌握小波分析的关键步骤。