系统辨识：算法解析与Matlab代码实践

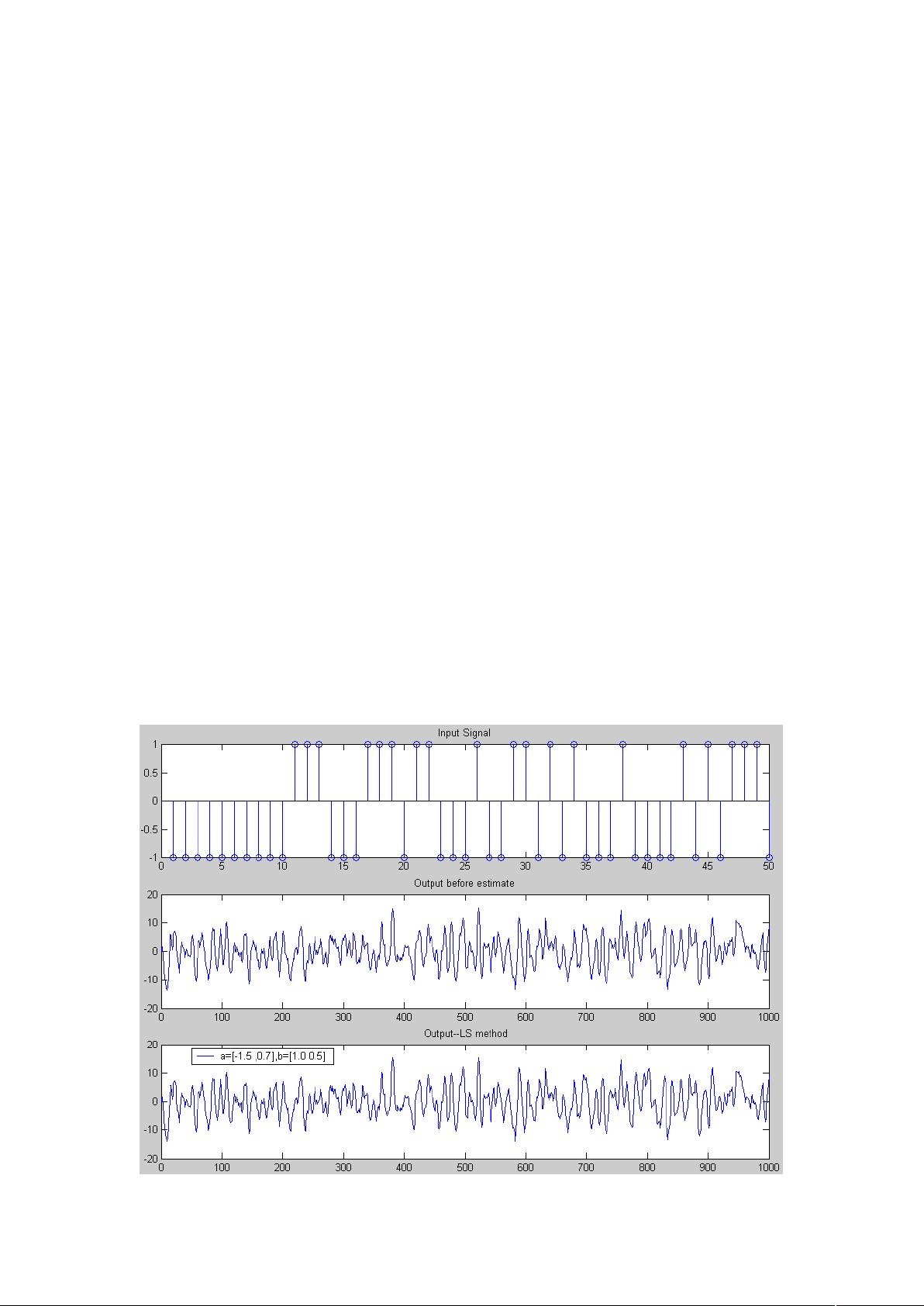
"该资源主要涉及系统辨识的理论与实践，通过朱豫才的著作讲解，配合Matlab代码实现。内容涵盖了系统离散化、ARX模型、递推算法以及相关性分析等方面，旨在帮助学习者理解并掌握系统辨识技术。在离散化方面，使用了MATLAB的simulink工具，通过linmod和c2d函数将连续系统转化为离散系统。此外，还展示了ARX模型的构建和求解，包括最小二乘法和递推最小二乘法的应用。" 在系统辨识中，首先需要了解的是**系统离散化**，这是将连续时间系统转换为离散时间系统的过程，这对于数字计算机处理至关重要。在给定的代码中，通过MATLAB的simulink建立模型，并利用`linmod`获取状态空间参数a、b、c、d，然后使用`ss2tf`将状态空间模型转化为传递函数，最后通过`c2d`函数以指定的采样时间Ts（这里是0.001秒）将系统离散化。 接下来，我们讨论**ARX（AutoRegressive with eXogenous input）模型**，这是一种广泛用于系统辨识的线性时不变模型。ARX模型假设输出可以由输入信号的历史值和当前的噪声表示，即y(t)=θ1u(t-1)+θ2u(t-2)+...+θnu(t-n)+e(t)，其中e(t)是零均值白噪声，θi为模型参数。示例代码中展示了如何生成PRBS（伪随机二进制序列）作为输入信号，并通过最小二乘法和递推最小二乘法估计ARX模型的参数。 **最小二乘法**是一种常用的数据拟合方法，用于在给定一组观测数据的情况下，找到最佳的参数估计。在系统辨识中，它被用来求解ARX模型的参数。给定的代码中，通过`idinput`生成PRBS输入信号，添加随机噪声，然后利用最小二乘法计算模型参数。 此外，**递推最小二乘法**（RLS，Recursive Least Squares）是一种在线学习算法，能够在每次新数据到来时实时更新模型参数，适用于大数据流或实时应用。虽然代码没有显示RLS的具体实现，但在实际应用中，RLS可以更高效地处理大量数据，特别是在数据流不断变化的情况下。 最后，**相关性分析**是系统辨识中的一个重要工具，用于评估输入输出信号之间的关系强度。在ARX模型的构建过程中，输入信号的选取和噪声的特性通常会通过相关性分析来确定，以确保模型的准确性。 总结来说，该资源提供了一个全面的系统辨识教程，从理论到实践，涵盖了关键的系统离散化、ARX模型构建和求解，以及相关性分析等概念，结合MATLAB代码实例，有助于深入理解和应用系统辨识技术。