JavaScript浮点数运算误差解析与应对策略

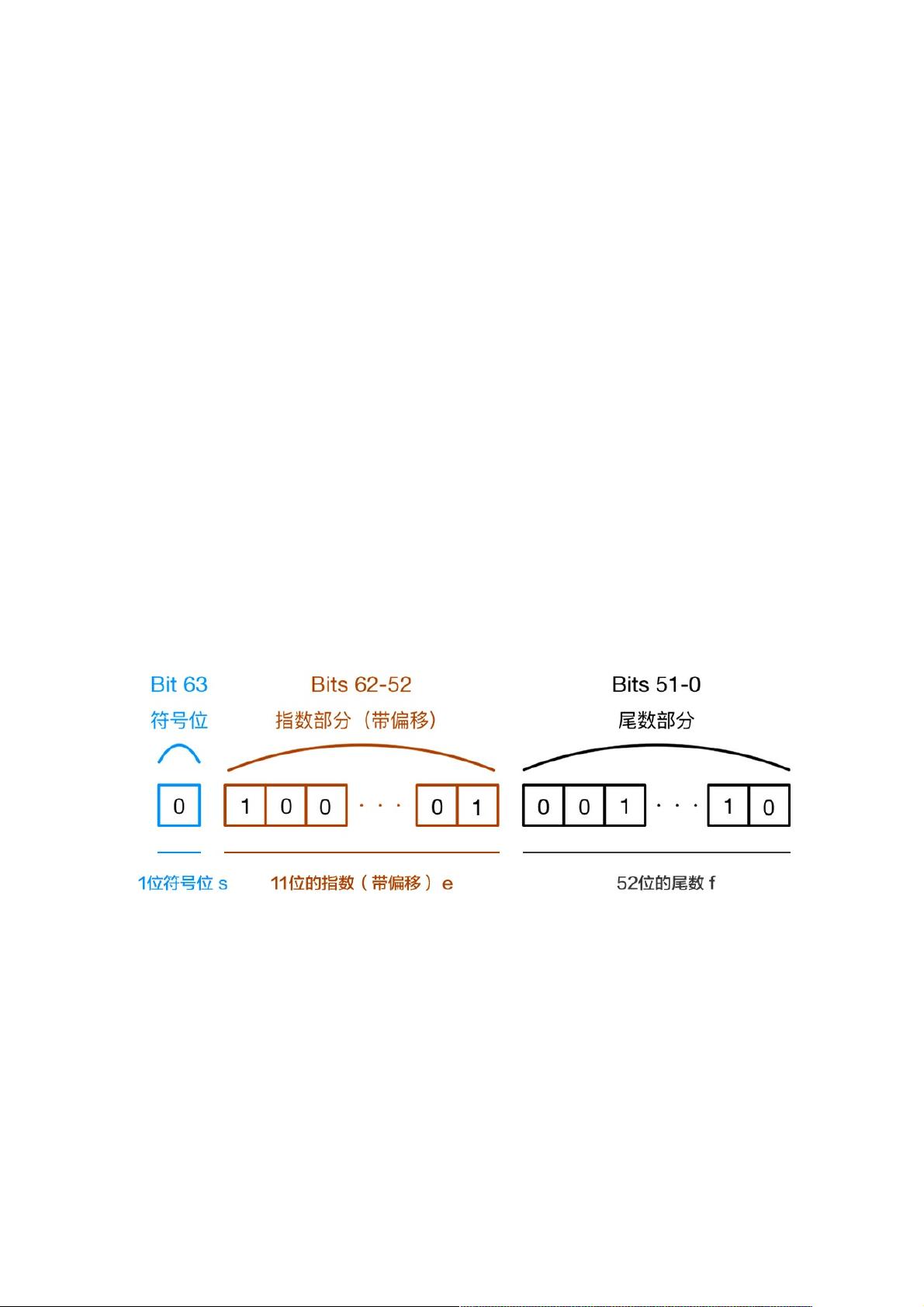
"JavaScript的浮点数运算存在精度问题，根源在于JavaScript使用了IEEE754标准的64位双精度浮点数表示数字。" 在JavaScript中，所有的数字（包括整数和浮点数）都是Number类型，并且以64位浮点数的形式存储。这种表示方法虽然适用于大多数计算，但在处理特定的浮点数运算时，可能会出现精度丢失的情况，导致计算结果不准确。这是因为64位浮点数的存储方式不能精确地表示某些十进制分数。 浮点数的存储由三部分组成：符号位、指数位和小数位。64位浮点数的分配是这样的： 1. 符号位：占1位，0代表正数，1代表负数。 2. 指数位：占11位，存储指数部分，通常会有一个偏移值（如1023）。 3. 小数位：占52位，存储小数部分，即有效数字。 IEEE754标准规定，浮点数在二进制转换过程中，会进行规范化处理，使得小数点前至少有一个非零数字，这会导致一些十进制数无法精确表示。例如，0.1在二进制下无法精确表示，因此在JavaScript中`0.1 + 0.2`并不等于我们期望的`0.3`，而是接近但不完全等于`0.30000000000000004`。 这种精度问题不仅出现在加法中，减法、乘法和除法也同样受到影响。例如： - 加法：`0.7 + 0.1` 结果是 `0.7999999999999999`，而不是 `0.8`。 - 减法：`1.5 - 1.2` 结果是 `0.30000000000000004`，而非 `0.3`。 - 乘法：`19.9 * 100` 结果是 `1989.9999999999998`，而不是 `2000`。 - 除法：`0.3 / 0.1` 结果是 `2.9999999999999996`，而非 `3`。 解决精度问题的方法有几种： 1. **四舍五入**：可以使用`Math.round()`、`Math.floor()`或`Math.ceil()`对结果进行四舍五入处理。 2. **字符串操作**：将数字转换为字符串，通过字符串拼接来处理金额等需要精确表示的场景。 3. **使用库**：利用如`decimal.js`或`big.js`等专门处理高精度计算的库。 4. **避免直接比较浮点数**：在判断相等性时，应该设定一个很小的误差范围（如`epsilon`），判断两个数的差是否小于这个范围，而非直接比较是否相等。 理解JavaScript中浮点数的精度问题是至关重要的，特别是在金融计算、物理模拟或其他需要精确数值的场景中。开发者应了解这一特性，并采取适当的策略来规避或补偿精度误差。