"Mathematica自定义函数PPT学习教案：一元、多元函数定义与应用"

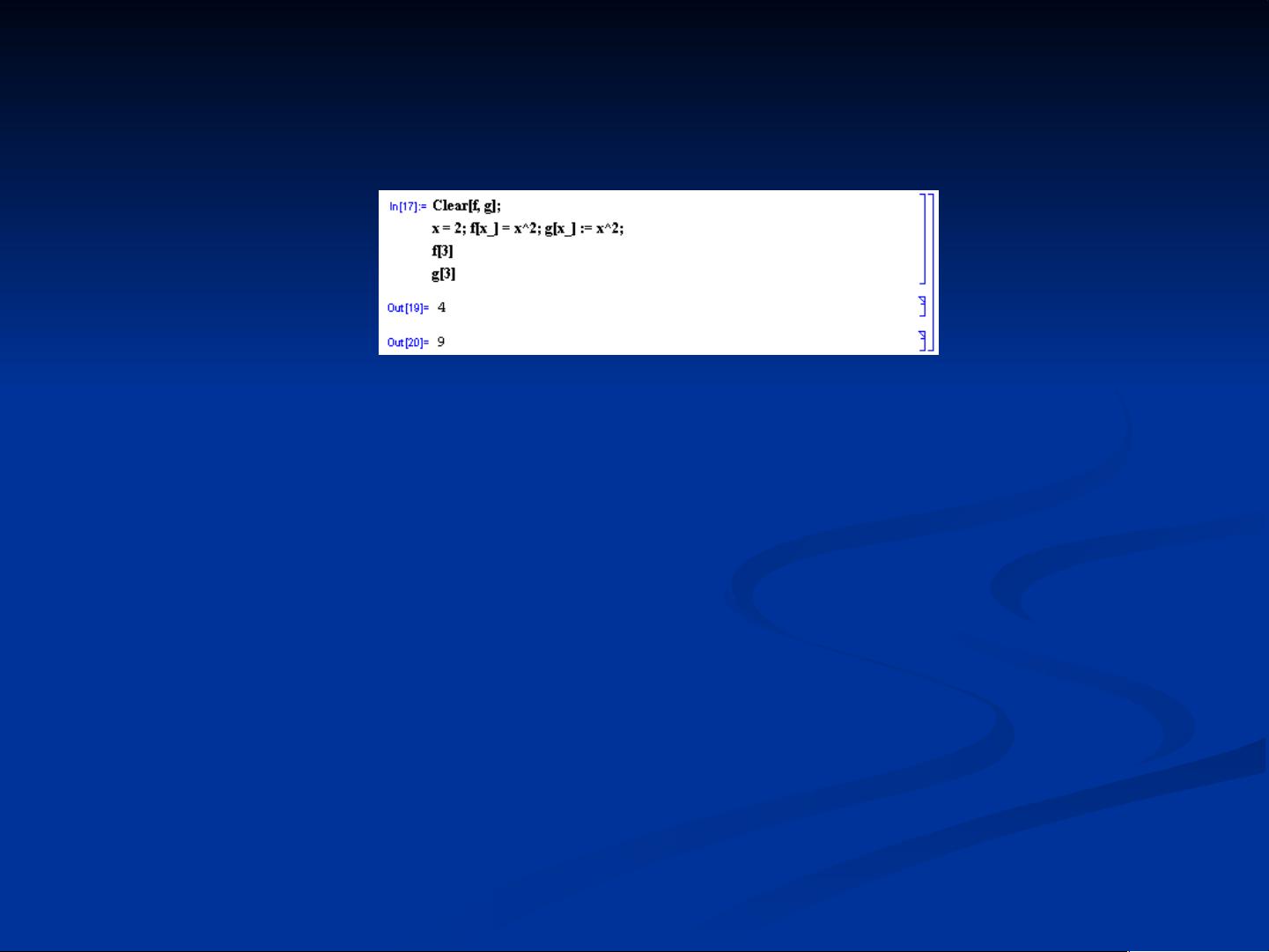
5.1 自定义函数 在之前的学习中，我们已经了解了Mathematica系统中提供的各种函数，这些函数都是由系统给出定义、明确功能，并且可以直接供用户调用。然而，在实际问题中，可能会遇到一些特殊的函数，这些函数在系统中并没有定义。在这种情况下，用户就需要自己来给出函数的定义，以便在后续的使用中更加方便。这就是我们即将介绍的自定义函数。 5.1.1 自定义一元函数 自定义一元函数的方法如下：我们可以使用表达式 f[x_] := 自选表达式 来定义函数，例如 f[x_] := 2x+3。需要注意的是，Mathematica系统中使用方括号作为自变量的符号，而在数学中常用的函数定义中使用的是圆括号，因此在定义函数时需要注意将圆括号换为方括号，即 f[x_]=2*x+3。可以看到，在这里主要的差别在于自变量的表示方式。 5.1.2 自定义多元函数 除了自定义一元函数之外，我们还可以对多元函数进行自定义。多元函数的定义方法与一元函数相似，不同之处在于需要指定多个自变量。例如，我们可以使用表达式 f[x_,y_]:=x^2+y^2 来定义一个包含两个自变量的函数。 5.1.3 自定义函数的保存与重新调出 在对函数进行自定义之后，我们可以将这些函数保存起来，以便在以后的使用中重新调用。通过Mathematica系统提供的保存功能，我们可以将自定义函数保存在特定的位置，然后在需要的时候重新调出来使用。 5.2 函数的应用 通过上面的学习，我们已经掌握了如何在Mathematica系统中进行自定义函数的操作。接下来，我们将学习如何应用这些自定义函数来解决实际的数学问题。在数学建模和问题求解中，函数的应用是非常重要的，而自定义函数的灵活运用可以帮助我们更加高效地解决各种问题。 通过学习本课内容，我们不仅了解了如何在Mathematica系统中进行自定义函数的操作，还学会了如何对这些函数进行应用，这将为我们将来的学习与工作提供更加便利的数学工具。希望大家能够努力学习，掌握这些知识，并在实际的问题中加以运用。