一维与二维抛物型偏微分方程的有限差分法

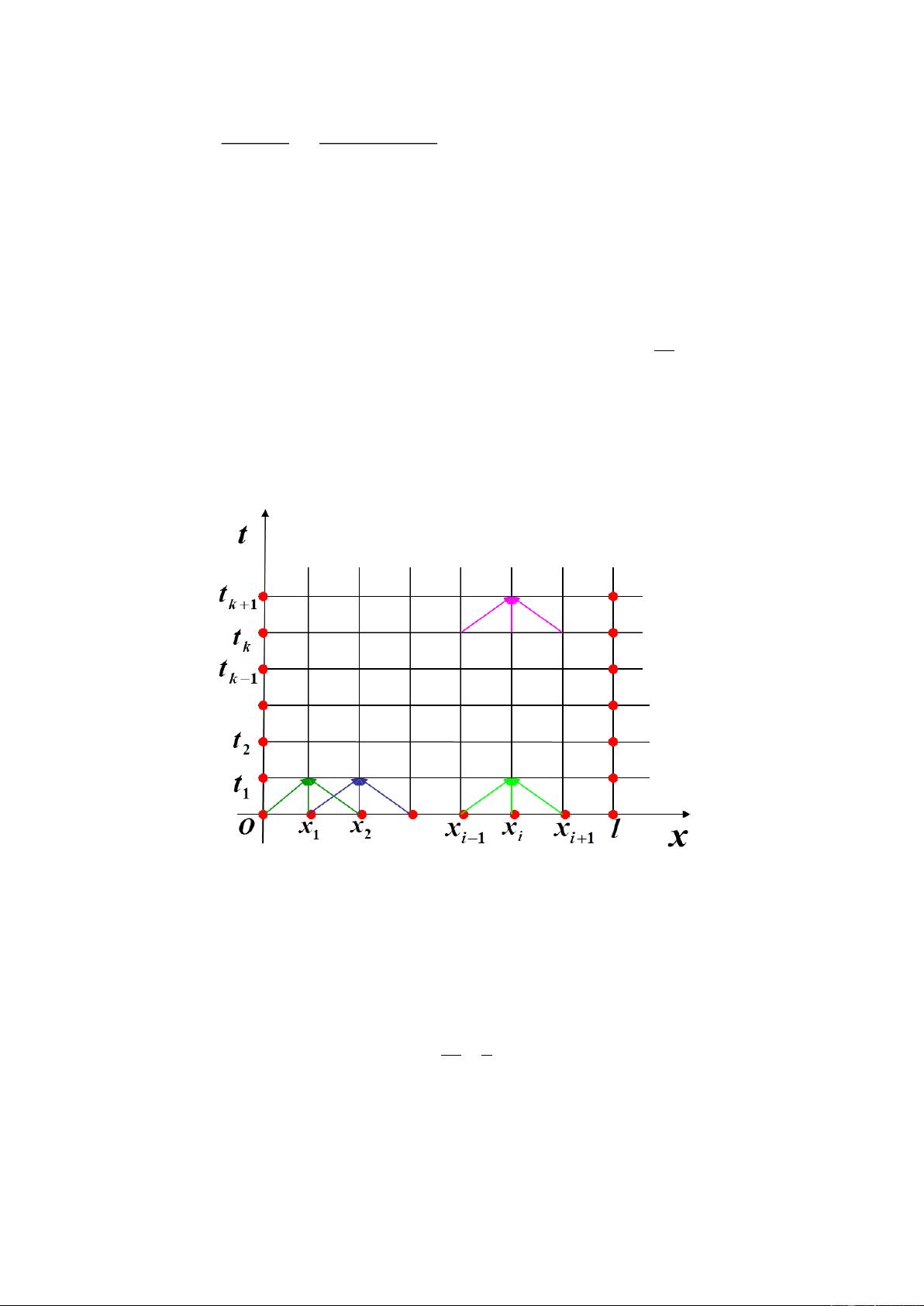
"本文主要介绍了抛物型偏微分方程的有限差分法，重点关注了一维空间下的一维抛物型方程及其在二维空间的推广，以及两种常见的数值求解方法：向前欧拉法。文章适用于对偏微分方程数值解有兴趣的读者，特别是对Python编程和数值计算有一定基础的学习者。" 抛物型偏微分方程在物理学中有广泛的应用，如导热问题。一维空间中的抛物型方程描述了长度为1、两端绝热的均匀细杆内部温度分布，其中方程形式包括时间和空间的二阶偏导数。边界条件和初始条件分别给出了温度分布的约束。 向前欧拉法是一种常用于求解这类方程的数值方法，它包括以下三个步骤： 1. 区域离散化：将空间和时间划分为等间隔的网格，每个网格点上都有对应的温度近似值。空间步长为h，时间步长为τ，网格节点为(i, k)xt，温度函数在该点的近似值为uk。 2. 离散方程：将偏微分方程对时间和空间进行离散化处理，形成一组代数方程。离散后的方程保留了原方程的基本结构，但用网格点上的温度函数代替了连续函数。 3. 差分近似：利用差分公式来近似偏导数。对于时间的一阶偏导数，采用向前差分，即用当前时间步的值减去前一时间步的值，除以时间步长τ，以此来逼近导数值。 向前欧拉法简单易懂，但存在稳定性问题，因为它是显式方法，对时间步长τ有严格的限制（Courant-Friedrichs-Lewy条件）。当τ过大时，解可能会变得不稳定。尽管如此，它仍是数值分析初学者和工程师常用的一种基础方法，尤其在教学和简单问题的求解中。 在实际应用中，通常会使用更高级的方法，如向后欧拉法、迎风差分、 Crank-Nicolson法或者隐式多步方法，这些方法能提供更好的稳定性和精度，但计算复杂度也会相应增加。对于二维空间的抛物型方程，处理方式类似，需要在两个空间维度上都进行离散化，得到一个更大的离散方程组。 为了实现这些算法，可以借助Python编程语言，结合科学计算库如NumPy和SciPy，编写数值求解程序。通过编程，不仅可以求解特定问题，还可以探索不同参数对解的影响，从而加深对偏微分方程数值解的理解。