红黑树详解:平衡二叉搜索树的理论与实践
需积分: 9 186 浏览量
更新于2024-09-07
收藏 149KB DOC 举报
"这篇资料主要介绍了红黑树这一数据结构,包括其基本概念、性质、插入和旋转操作,以及在维护平衡方面的重要性。"
红黑树是一种自平衡的二叉搜索树,它在二叉搜索树的基础上进行了优化,以确保在最坏情况下也能保持高效的查找、插入和删除操作。红黑树的核心特性是每个节点都有一个额外的“颜色”属性,可以是红色或黑色,并且遵循以下五条性质:
1. 根节点是黑色。
2. 所有叶子节点(叶节点即空节点,通常用NIL表示)都是黑色。
3. 如果一个节点是红色,则它的两个子节点都是黑色。
4. 对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数量的黑色节点。
5. 插入的所有新节点都是红色,这有助于保持性质4。
插入操作:
在红黑树中插入节点时,首先按照二叉搜索树的规则找到插入位置。然后,新插入的节点被标记为红色,这是因为红色节点不会违反红黑树的性质4,即路径上黑色节点的数量保持不变。但是,插入红色节点可能会导致违反其他性质,所以需要进行调整,通常是通过旋转和重新着色来修复。
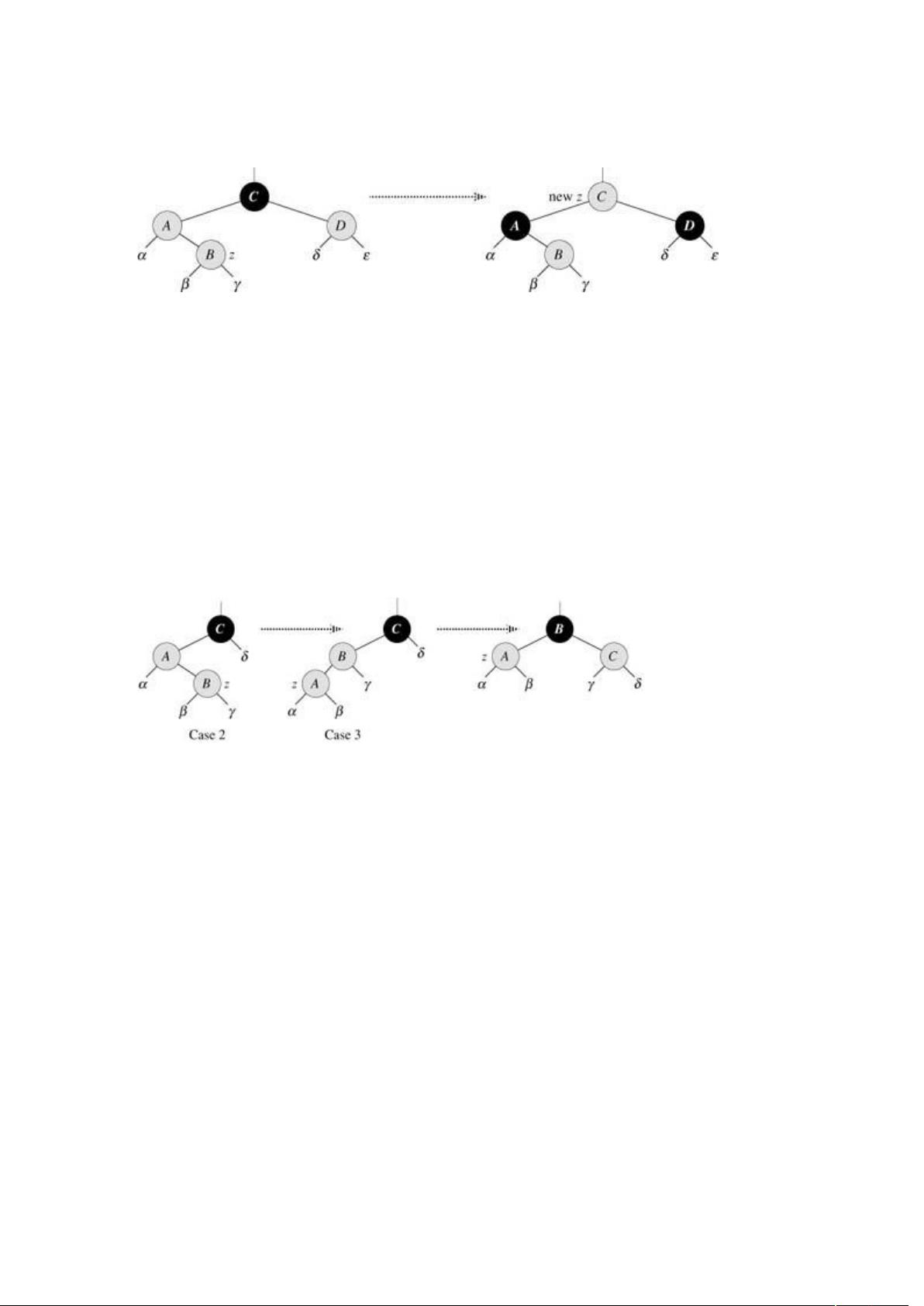
旋转操作:
- 左旋(Left-Rotate):将节点x向左下方移动,x的右子节点y替换x的位置,y的左子节点成为x的新右子节点。
- 右旋(Right-Rotate):与左旋相反,将节点x向右下方移动,x的左子节点y替换x的位置,y的右子节点成为x的新左子节点。
这两种旋转操作可以保持二叉搜索树的性质,同时在红黑树的调整过程中起到关键作用。在插入后,可能需要通过单旋转或双旋转(先左旋再右旋或先右旋再左旋)来恢复红黑树的性质。
删除操作:
红黑树的删除操作比插入更复杂,因为需要考虑更多的情况,如删除节点的颜色、是否有子节点等。删除节点可能导致红黑树的性质被破坏,因此通常会涉及节点颜色的重新分配、旋转甚至重新插入已删除节点的兄弟节点来维持平衡。
总结来说,红黑树是一种高效的数据结构,通过颜色属性和特定的旋转策略来保证操作的平均时间复杂度为O(log N),从而在动态数据集合中提供快速访问。对于理解和实现红黑树,掌握其基本性质、插入和删除操作及其后的平衡调整是至关重要的。
2022-10-17 上传
2014-03-14 上传
2015-05-07 上传
2015-06-03 上传
2012-04-19 上传
2022-08-03 上传
2012-02-28 上传
2022-09-21 上传
2019-03-05 上传
漂洋过海95
- 粉丝: 17
- 资源: 2
最新资源
- Aspose资源包:转PDF无水印学习工具
- Go语言控制台输入输出操作教程
- 红外遥控报警器原理及应用详解下载
- 控制卷筒纸侧面位置的先进装置技术解析
- 易语言加解密例程源码详解与实践
- SpringMVC客户管理系统:Hibernate与Bootstrap集成实践
- 深入理解JavaScript Set与WeakSet的使用
- 深入解析接收存储及发送装置的广播技术方法
- zyString模块1.0源码公开-易语言编程利器
- Android记分板UI设计:SimpleScoreboard的简洁与高效
- 量子网格列设置存储组件:开源解决方案
- 全面技术源码合集:CcVita Php Check v1.1
- 中军创易语言抢购软件:付款功能解析
- Python手动实现图像滤波教程
- MATLAB源代码实现基于DFT的量子传输分析
- 开源程序Hukoch.exe:简化食谱管理与导入功能