卷积码大数逻辑译码原理与应用

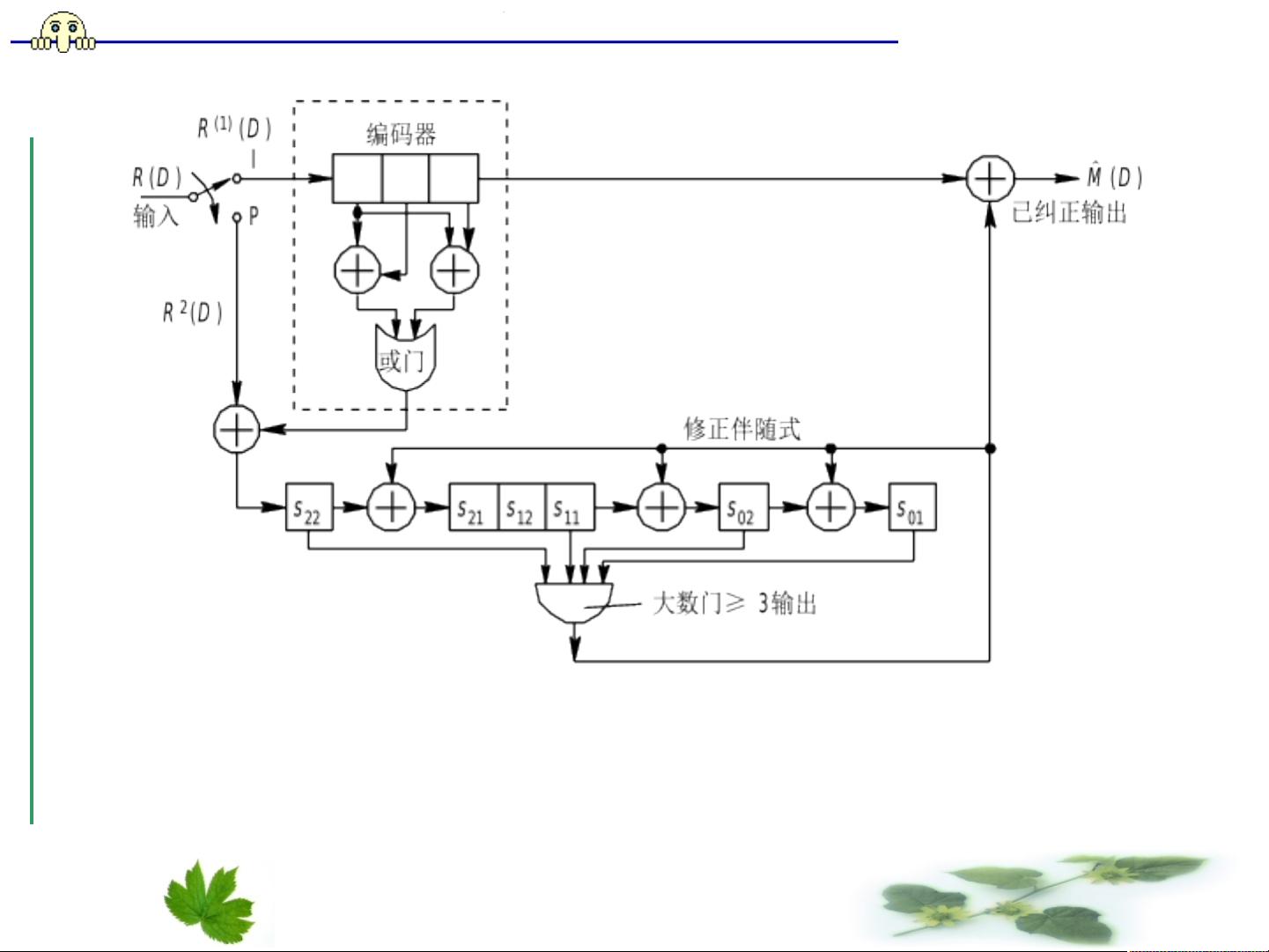
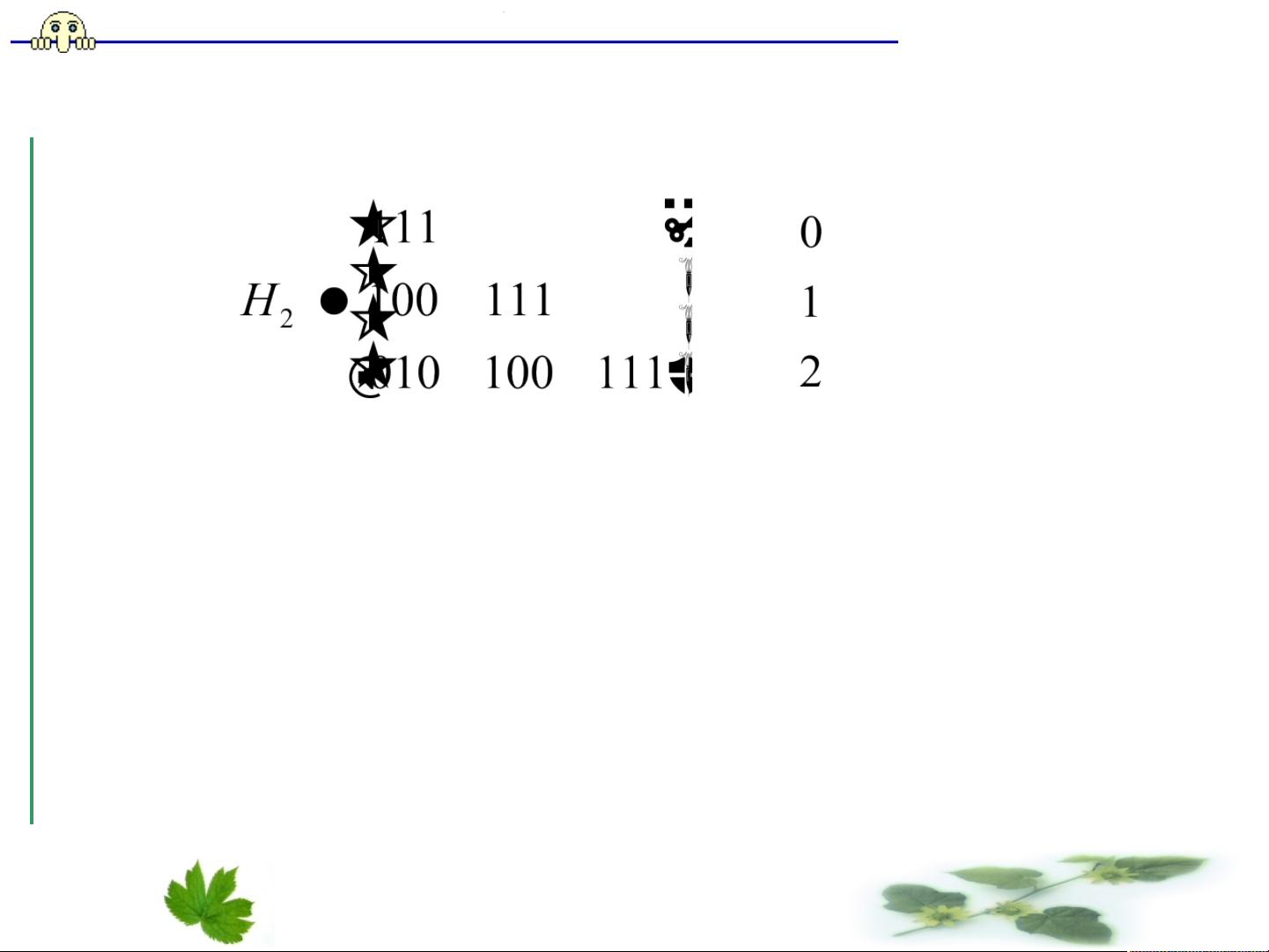
"卷积码的大数逻辑译码方法在信息与通信领域中是重要的纠错编码技术，主要用于纠正随机错误和突发错误。大数逻辑译码由梅西在1963年提出，鲁滨逊等人在1967年进一步发展，特别是在自正交码和可正交码的应用上。卷积码的译码方法主要包括代数译码，其中大数逻辑译码是最主要的一种。这种译码方式与循环码的大数逻辑译码原理相似，但主要针对卷积码的特点进行设计。 卷积码的一大优势在于，对于(n0, k0, m)系统的码字，任何连续m+1个码段内的码元都遵循初始截短码的校验矩阵所确定的校验关系。因此，如果第0子组的k0个码元可以构成J个正交一致校验和式，那么就能使用大数逻辑译码来纠正最多t=［J/2］个随机错误，其中t是可纠正的错误数。通常，译码约束度是m+1，并且大数逻辑译码常采用反馈机制。 自正交码是卷积码的一种类型，它意味着码字的各个部分相互正交，即在特定条件下，码字的不同部分之间不存在非零的内积。例如，考虑一个(2,1,6)系统卷积码，其子生成元为g(1,1)和g(1,2)，对应的校验矩阵H可以用来计算伴随式S。通过分析S的各个分量，可以看出有4个方程（s01，s21，s51，s61）与e01码元位正交，这样就可以单独确定e01的错误值，而无需其他码元的信息。这个特性使得自正交码在大数逻辑译码中表现出色，因为它允许我们直接根据校验关系确定错误位置。 定义11.1.1强调了自正交码的特性，即对于一个(n0, k0, m)系统卷积码，如果能够直接从H矩阵的某些行（无需进行线性组合）构造出Ji个分量的一致校验和式，那么这个码就是自正交的。这意味着自正交码的错误检测和校正能力较强，特别适合应用在存在随机错误和突发错误的通信环境中。 此外，虽然这里的描述主要关注了系统码的大数逻辑译码，卷积码还包含非系统码的情况，非系统码的大数逻辑译码方法将在后续内容中讨论。非系统码与系统码的主要区别在于，系统码的码字可以直接由信息序列得到，而非系统码则需要经过更复杂的转换过程。 总结起来，大数逻辑译码是卷积码的一种高效译码策略，尤其适用于自正交码。这种译码方法利用卷积码的结构特性，能够在满足一定条件时有效地纠正随机错误和突发错误，提高了通信的可靠性。对于信息与通信工程而言，理解和掌握卷积码的大数逻辑译码对于设计和优化通信系统至关重要。