遗传算法求解函数极值:实例与实验结果
版权申诉
186 浏览量
更新于2024-07-03
收藏 1.2MB PDF 举报
"遗传算法求函数极值的作业详细解析"
一、遗传算法基础
遗传算法是一种模拟自然选择和遗传过程的全局优化方法,用于解决复杂的优化问题。它主要用于寻找函数极值,特别是对于那些传统优化算法难以处理的非线性、多模态或多维问题。在这个特定的作业中,目标是使用遗传算法来求解函数f(x) = xsin(10πx) + 2.0在区间[-1, 2]上的最大值。
二、实例步骤
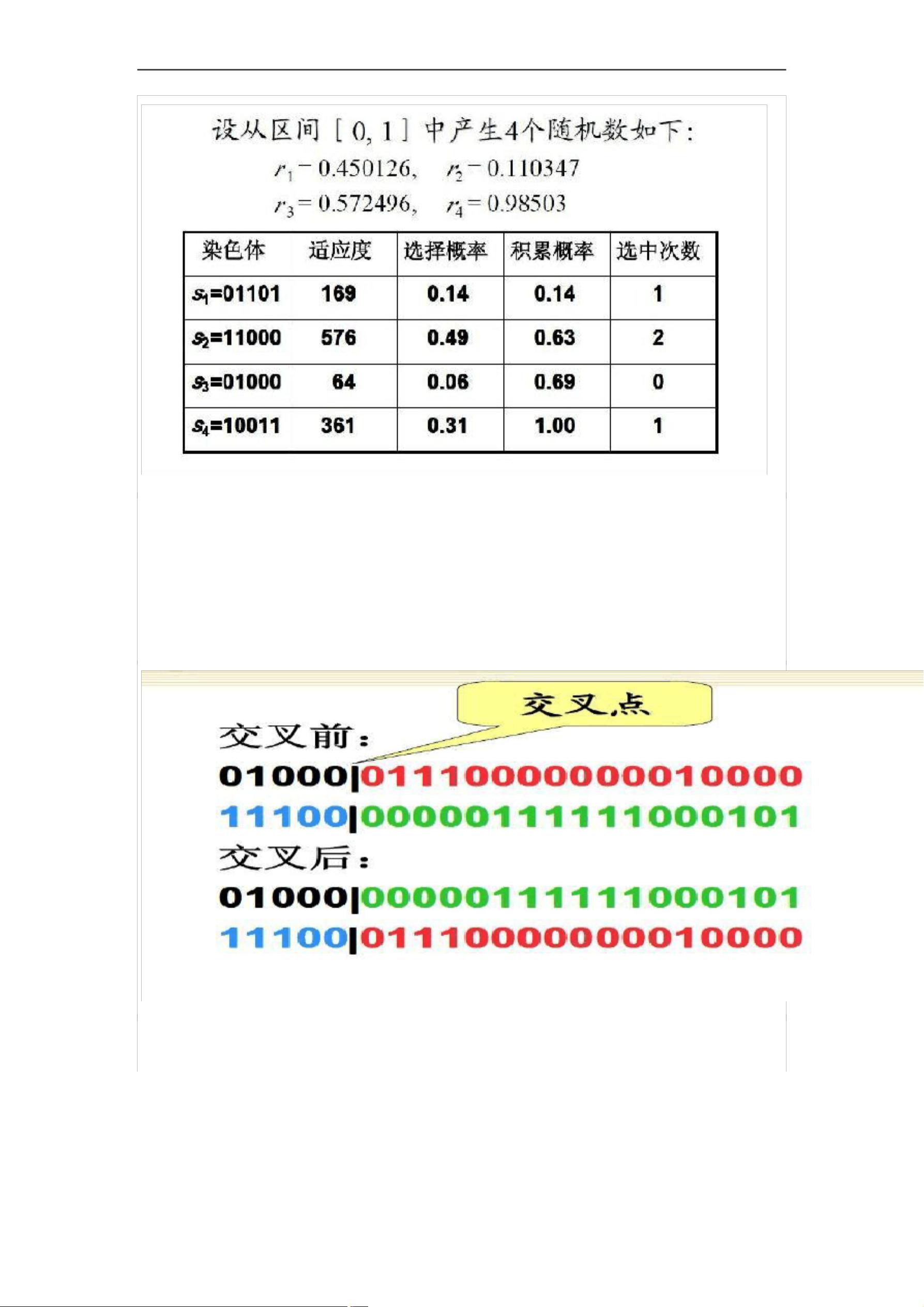
1. 初始种群生成:种群由一系列可能的解(染色体)组成,这里给出了四个初始种群成员s1到s4,它们是用二进制表示的数字,如s1=13(01101)。这些种群代表了对目标函数可能的解空间中的潜在位置。
2. 适应度计算:适应度函数用来评估个体解的质量,这里假设适应度为f(s) = s^2。计算后,个体s1到s4的适应度分别为169, 576, 64, 和 361。
3. 选择操作:选择过程基于适应度值,高适应度的个体更有可能被选中。选择概率通过累积概率计算得出,这决定了哪些个体在下一代种群中有更高的生存机会。
4. 交叉操作:单点交叉是遗传算法的基本操作之一,通过对两个父代个体在随机选择的交叉点进行基因交换,产生新的个体。这个过程模拟了遗传的重组过程。
5. 变异操作:变异是另一个重要步骤,通过引入随机性,增加了种群的多样性,防止陷入局部最优。变异点的选择也是随机的,可能会改变种群中的某些基因。
6. 迭代过程:不断重复计算适应度、选择、交叉和变异,直到达到预设的终止条件,如达到一定代数或适应度值达到足够高的阈值。
三、实现步骤与代码
在源代码中,使用C++编程语言实现了遗传算法的上述步骤。包括种群初始化(规模为NUMBER50),基因数量(GENE_NUMBER10000),以及交叉和变异概率的设置。核心部分是使用随机数生成器(如time库)来模拟自然选择过程。
四、实验结果
通过执行这段代码,算法会逐步优化种群,寻找函数f(x)的最大值。实验结果展示了算法找到的局部或全局最优解,以及是否达到预期的最大值。在实际应用中,可能需要多次运行以获得稳定的结果,因为遗传算法是概率驱动的,每次执行可能产生不同的结果。
总结,遗传算法在本作业中作为一种强大的全局优化工具,应用于求解复杂的函数极值问题,展示了其在处理非线性和多维搜索中的潜力。通过实例介绍,学生可以深入理解遗传算法的工作原理及其在实际问题中的应用。
2021-12-18 上传
2021-11-26 上传
2024-04-11 上传
2021-05-23 上传
2022-01-20 上传
2019-06-06 上传
2022-11-20 上传
2021-11-23 上传
2022-01-01 上传
苦茶子12138
- 粉丝: 1w+
- 资源: 6万+
最新资源
- Python中快速友好的MessagePack序列化库msgspec
- 大学生社团管理系统设计与实现
- 基于Netbeans和JavaFX的宿舍管理系统开发与实践
- NodeJS打造Discord机器人:kazzcord功能全解析
- 小学教学与管理一体化:校务管理系统v***
- AppDeploy neXtGen:无需代理的Windows AD集成软件自动分发
- 基于SSM和JSP技术的网上商城系统开发
- 探索ANOIRA16的GitHub托管测试网站之路
- 语音性别识别:机器学习模型的精确度提升策略
- 利用MATLAB代码让古董486电脑焕发新生
- Erlang VM上的分布式生命游戏实现与Elixir设计
- 一键下载管理 - Go to Downloads-crx插件
- Java SSM框架开发的客户关系管理系统
- 使用SQL数据库和Django开发应用程序指南
- Spring Security实战指南:详细示例与应用
- Quarkus项目测试展示柜:Cucumber与FitNesse实践