经典网络流模型详解与实例解析

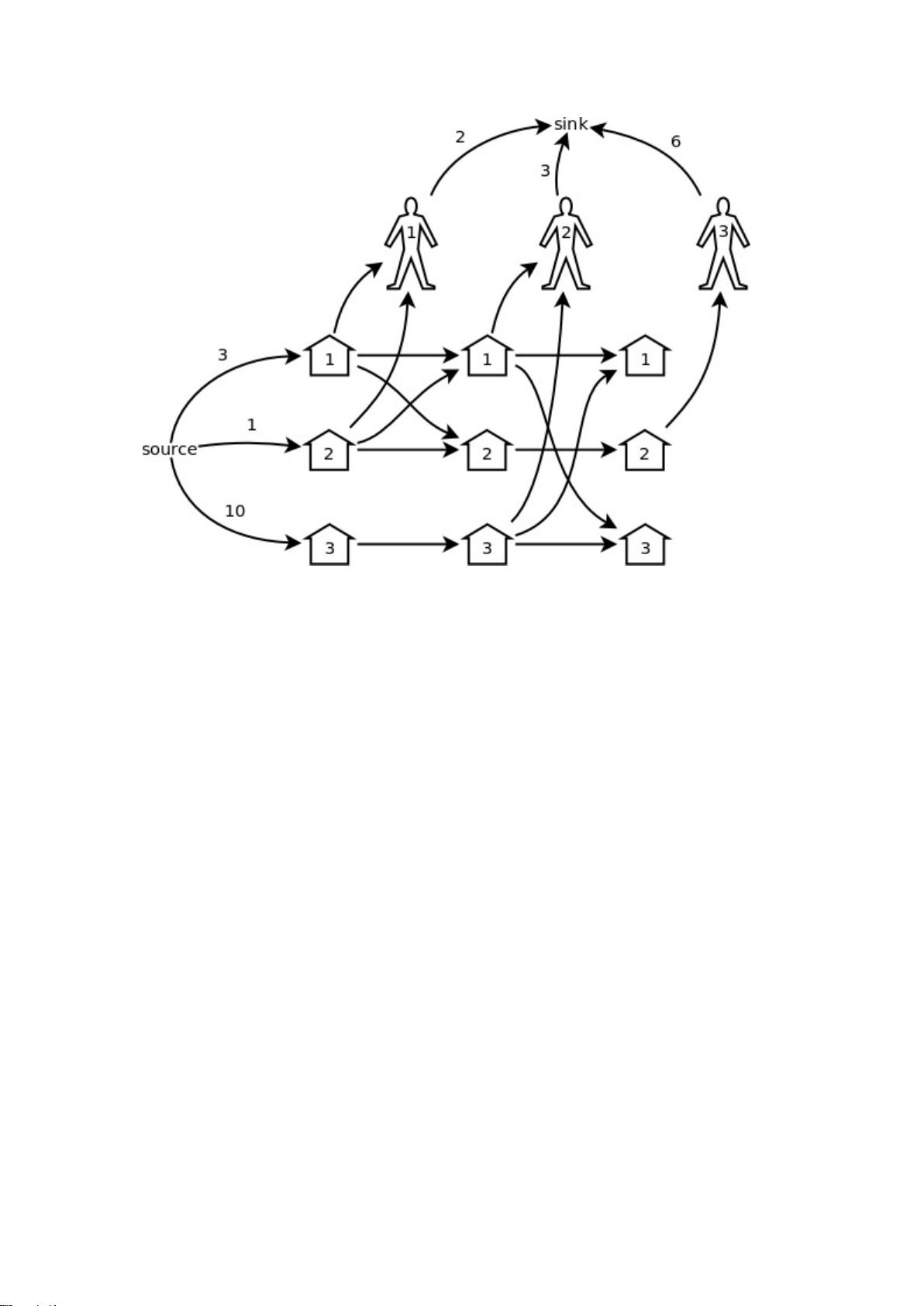
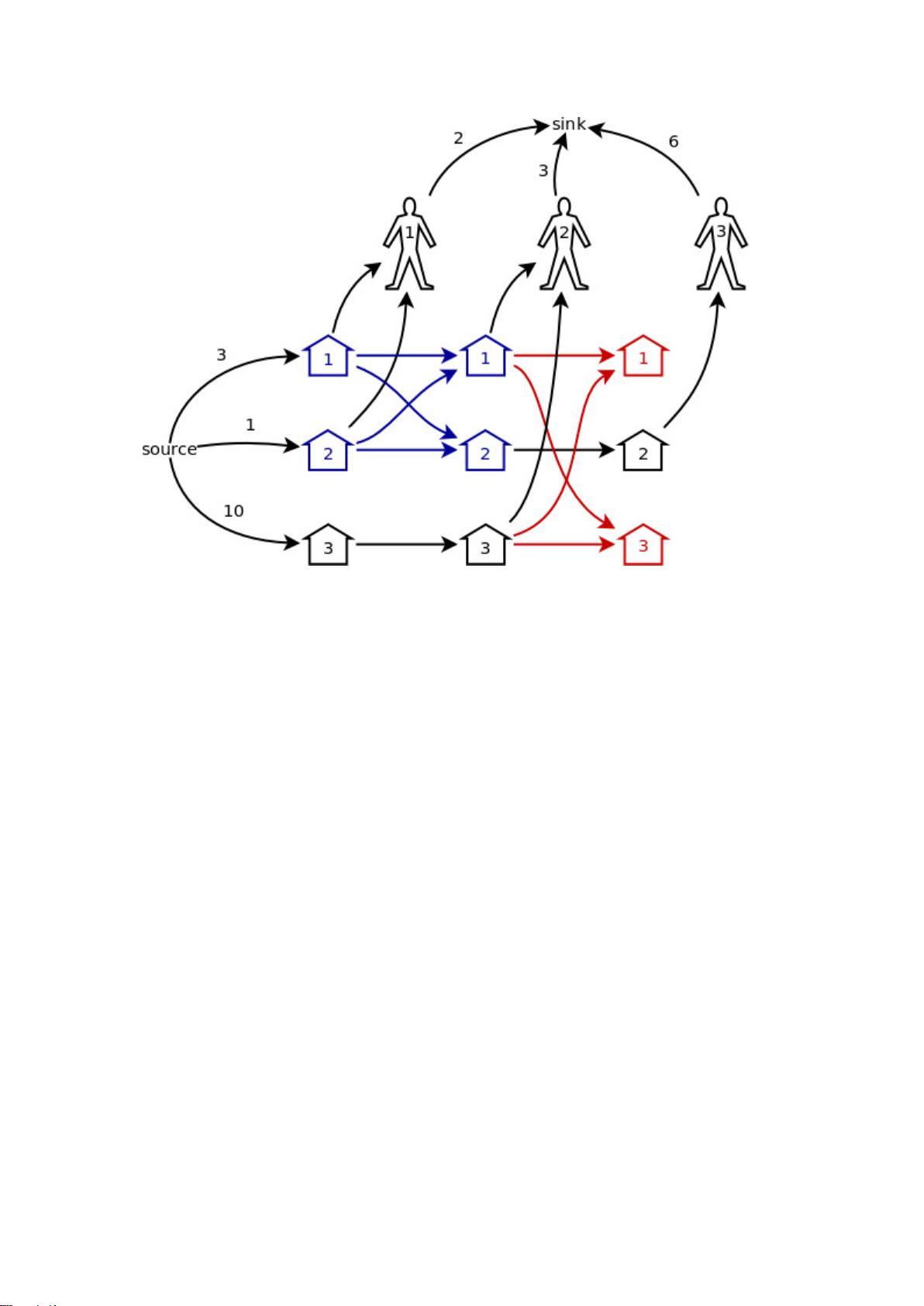
网络流建模是图论在计算机科学中的一个重要应用，它主要关注如何有效地分配或传输在网络图中的资源，如数据流量、物质等，同时满足特定的约束条件。这份汇总涵盖了多个经典的网络流问题，旨在帮助学习者理解和解决实际问题。 1. **最大流**：这个部分首先介绍的是最大流问题，例如POJ1149 "PIGS"。该题描述了M个猪圈与N个顾客之间的互动，每个顾客可以购买一定数量的猪，并且可以将猪在打开的猪圈间转移。目标是确定在顾客离开后，如何最大化整体的销售量，同时考虑每个顾客的购买上限和猪圈的交换操作。 2. **路径相关问题**：如" Sightseeing tour"（POJ1637）和"How Many Shortest Path" (ZOJ2760)，涉及寻找最短路径的数量，这可能是在寻找最优路径或路径优化过程中遇到的问题。 3. **最小割**：这部分包括HOJ2634 "How to earn more" 和 HOJ2713 Matrix1，最小割是求解网络中分割图的最少边数，常用于分析网络结构和资源分配的效率。 4. **费用流**：最小费用流问题如"Budget" (POJ2396) 和 "Stone IV" (HOJ2543)，涉及到在满足容量限制的同时，寻找成本最低的资源分配方案。 5. **经典算法**：如 "The Chinese Postman Problem" (HOJ2739) 是一个著名问题，涉及寻找一条路径，使得图中所有的边都被恰好经过一次，这在实际物流和通信网络设计中有广泛应用。 6. **其他问题**：例如 "Dining" (POJ3281) 和 "Candy" (JOJ2453) 描述了更贴近生活的场景，如餐厅座位安排和糖果分配，通过网络流模型解决实际生活中的优化问题。 7. **竞赛题目**：这份汇总还列出了来自ACM竞赛（如SPOJ）的题目，这些题目通常具有挑战性和实战性，可以帮助学习者提升算法设计和编程能力。 8. **总结与技巧**：每部分的小结部分可能对各个主题进行了总结，介绍了相关理论、常用算法（如 Ford-Fulkerson 方法）以及解题策略，帮助读者更好地理解和掌握网络流建模的核心概念。 通过学习这些模型，读者可以深入了解网络流的基本原理，掌握解决这类问题的关键技术和方法，为应对更复杂的实际问题打下坚实基础。